欧拉定理,费马小定理
证明之前写了这里就不再证明了
https://www.cnblogs.com/hky2023/p/19006833
但是由于每一个你愿都需要单独利用快速幂,计算n个逆元就需要nlog(mod),时间复杂度有点高,
下面就是引入一个递推公式可以利用快速求n前n个元素的逆元,时间复杂度是n
递推
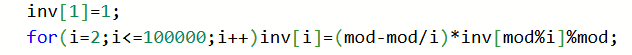
inv[i] 就是i的关于mod的乘法逆元
证明:mod = q * i + r, r = mod % i;
(1)q * i + r =(同余)0 MOD mod,
我们需要求i的逆元inv[i]: i * inv[i] =(同余)1 MOD mod;
由(1)式两边同时乘以inv[i] * inv[r]得到:q * i * inv[i] * inv[r] + r * inv[i] * inv[r] =(同余) 0 MOD mod;
由于i * inv[i] = 1 MOD mod, r * inv[r] = 1 MOD mod;
可得q * inv[r] + inv[i] = 0 MOD mod -> inv[i] = -q * inv[r] MOD mod;
我们就可以使用同余号右边的式子进行递推了,但是存在一点就是右边的式子是负值,我们还需要一点变动:
inv[i] = (mod - q) * inv[r] MOD mod;这样一来给右边引入了一个mod * inv[r],由于是mod的倍数不影响取模后的值,所以值不变,由于q = mod / i【下取整】值取正了。
所以才有了图示递推公式。
所以我们只需要提前赋值一下inv[1] = 1,inv[0]是非法的,但是不会存在递推取inv[r], r=0的情况,因为题目一般选择的mod是质数,这样一来取余等于0要么就是1(我们提前帮他赋值,不会错误),要么就是mod自己(一般取不到)。
