当前位置：首页 > news >正文

分块莫队

news 2025/8/3 16:30:36

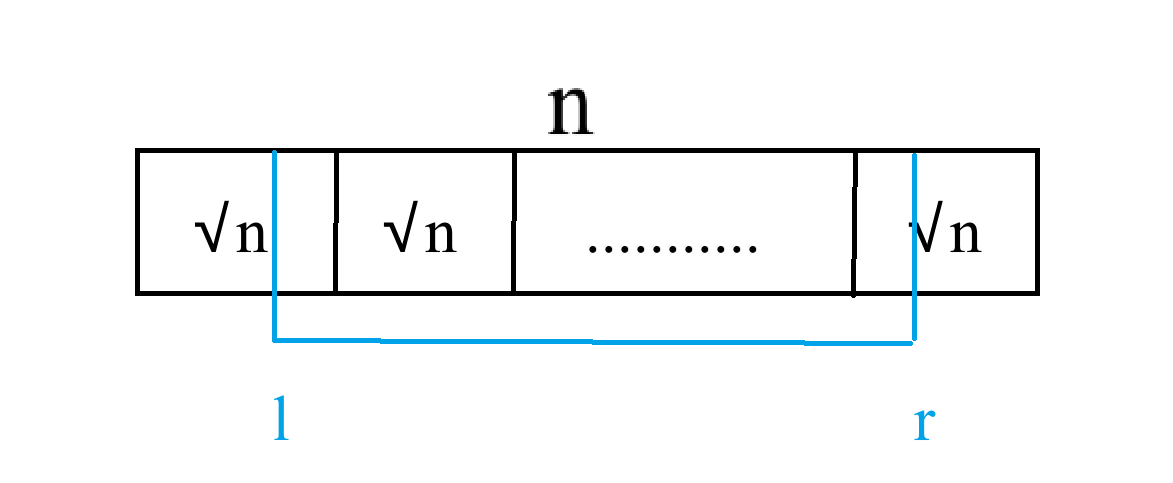
分块

分块思想

描述

具体来说，分块是一种思想，是一种不错的优化时间复杂度的方法。
一般是根据题意，将一段序列分成若干块，从而可以对每块操作，进而优化时间复杂度。

时间复杂度

一般来说，分块可以将时间复杂度由 $\mathcal O(n^2)$ 优化到 $\mathcal O(n \sqrt n)$。

例题1 Luogu P3870 开关

题意

给你一个 $01$ 序列，初始都为 $0$。对其进行两种操作：翻转一段区间和查询一段区间的 $1$ 的数量。

分块

~~经典的线段树问题。~~
考虑将整个序列分成若干块，每一块的大小为 $\sqrt n$。记录一个数组 $ct_i$ 表示第 $i$ 块的 $1$ 的数量。

修改
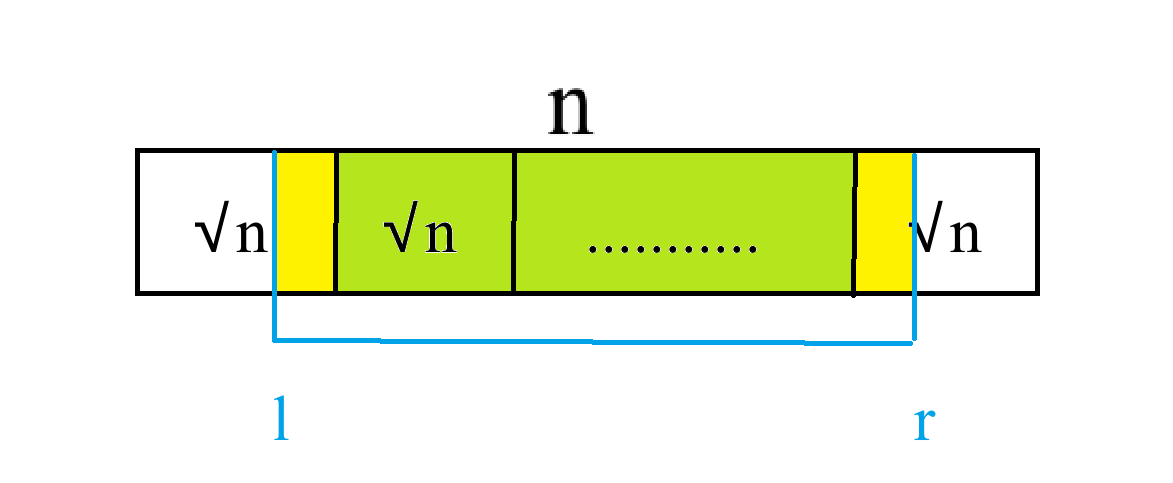
比如翻转区间 $[l, r]$。先将其对应到各个块中：

然后，对于分散在块中的两端（黄色部分），我们单独暴力更改这个块中的信息，同时更新 $ct$。时间复杂度 $\mathcal O(\sqrt n)$。
对于完整的块（绿色部分），我们记一个懒标记数组 $tag_i$，表示第 $i$ 块是否需要翻转。更新时，直接将 $tag_i$ 翻转，$ct_i$ 变为 $S - st_i$，其中 $S$ 是这块的长度。时间复杂度 $\mathcal O(\sqrt n)$。
查询
同理，我们可以如上处理询问。

块长为什么是 $\sqrt n$

设块长为 $L$，则有共 $\frac{n}{L}$块。
零散的块暴力复杂度 $\mathcal O(L)$，整块 $\mathcal O(\frac{n}{L})$。
总体时间 $\mathcal O(L+\frac{n}{L})$。
由均值不等式得：原式 $\ge 2 \sqrt {L \times \frac{n}{L}} = 2 \sqrt n$。
当 $L=\sqrt n$ 时取等，因此，当块长为 $\sqrt n$时，平均时间复杂度最小。

Code

Code

#include<bits/stdc++.h>using namespace std;#define get(x) ((x - 1) / S + 1) // 找到x对应的块
#define get_l(x) ((x - 1) * S + 1) // 第x块的左端点
#define get_r(x) min(n, x * S) // 第x块的右端点int n, m, S;
int ct[10005], tag[10005];
int a[100010];int main(){scanf("%d%d", &n, &m);S = sqrt(n); // 块长while(m --){int c, aa, b; scanf("%d%d%d", &c, &aa, &b);if(c == 0){if(get(aa) == get(b)){ // 位于同一块中int k = get(aa); ct[k] = 0; for(int i = get_l(k); i <= get_r(k); i ++) { // 暴力修改a[i] ^= tag[k]; // 懒标记下传if(i >= aa && i <= b) a[i] ^= 1;ct[k] += a[i]; // 更新} tag[k] = 0; // 懒标记清空} else {int k = get(aa); ct[k] = 0;for(int i = get_l(k); i <= get_r(k); i ++){ // 左边的暴力修改a[i] ^= tag[k];if(i >= aa) a[i] ^= 1;ct[k] += a[i];}tag[k] = 0;for(int j = get(aa) + 1; j < get(b); j ++){ // 完整的块ct[j] = (get_r(j) - get_l(j) + 1) - ct[j]; // 更新tag[j] ^= 1; // 懒标记更新}k = get(b); ct[k] = 0;for(int i = get_l(k); i <= get_r(k); i ++){ // 暴力修改右边的部分a[i] ^= tag[k];if(i <= b) a[i] ^= 1;ct[k] += a[i];} tag[k] = 0;}} else {if(get(aa) == get(b)){int k = get(aa), res = 0; for(int i = aa; i <= b; i ++) res += (a[i] ^ tag[k]); // 块内单独查询printf("%d\n", res);} else {int k = get(aa), res = 0;for(int i = aa; i <= get_r(k); i ++) res += (a[i] ^ tag[k]); // 左边暴力for(int j = get(aa) + 1; j < get(b); j ++) res += ct[j]; // 完整查询k = get(b);for(int i = get_l(k); i <= b; i ++) res += (a[i] ^ tag[k]); // 右边暴力printf("%d\n", res);}}} return 0;
}

例题2 Luogu P5064 等这场战争结束之后

分析

对于连通块的维护，可以考虑使用并查集。但如果使用暴力查询第 $y$ 小，时间复杂度 $\mathcal O(nm)$，必然会爆掉。考虑如何优化。

为此，~~我们可以用平衡树~~，我们可以给权值（离散化后的）进行分块，同时开一个数组 $ct_{i, j}$ 记录第 $i$ 个点所在连通块位于分出来的第 $j$ 块的数量的多少。
这样一来，每次查询时的操作时间复杂度可以降到 $\mathcal O(\sqrt n)$，时间绰绰有余。

回滚

最让人头疼的回滚该怎么做呢？

这时候就需要用到一个叫做操作树的东西。顾名思义，就是把所有的操作建成一棵树。

我们以 $0$ 号节点为根，操作的类型为点权，若是普通操作 $i$，就把操作 $i - 1$ 向 $i$ 连一条单向边。若是回滚操作，就把第 $i$ 次操作接在回滚回的点 $x$ 上。由于除 $0$ 号节点外，所有的节点都有一个父亲，那么建出来的东西就是一棵树。

最后 $DFS$ 一边，求出答案即可。

注意事项

空间被卡时，可以适当用 $short$ 类型存储。
由于需要 $DFS$ 回溯，因此使用并查集时，不可路径压缩。
时间比较严，建议写快读快写。
并查集合并时，建议采用启发式合并。即将点数少的合并到点数大的，以减少时间复杂度。

Code

#include<bits/stdc++.h>using namespace std;const int N = 1e5 + 5, S = 3000;int n, Q, m, k;
int w[N], b[N], num[N]; //离散化
short iuy[N][N / S + 2]; // 在块中的在块中的数量（必须开short，不然空间会卡）
int fa[N], sz[N]; // 并查集
int number[N]; 
pair<pair<int, int>, int> q[N]; // 询问离线
int ans[N]; // 答案struct Node{int to, nxt;
} tr[N << 1];int hd[N << 1], idx;void add(int u, int v){tr[++ idx] = {v, hd[u]}, hd[u] = idx;
}void init(){for(int i = 1; i <= n; i ++) fa[i] = i, sz[i] = 1;
}int find(int x){ // 查找； 不要路径压缩if(x == fa[x]) return x;return find(fa[x]);
}void dfs(int u){int op = q[u].second, x = q[u].first.first, y = q[u].first.second;if(op == 1){ // 加入一条边x = find(x), y = find(y);if(x != y) {if(sz[x] > sz[y]) swap(x, y); fa[x] = y; sz[y] += sz[x]; // 启发式合并for(int i = 1; i <= m; i ++){ // 对于每一块分别更新iuy[y][i] += iuy[x][i];}	}}if(op == 3){x = find(x);if(y > sz[x]) ans[u] = -1;else {for(int i = 1; i <= m; i ++){if(y <= iuy[x][i]){ // 一块一块的找for(int j = (i - 1) * S + 1; j <= i * S; j ++){ // 单独查找if(find(num[j]) == x){-- y;if(y == 0) {ans[u] = b[j];break; } }} break;}y -= iuy[x][i];}}}	for(int i = hd[u]; i; i = tr[i].nxt){ // 继续操作dfs(tr[i].to);}if(op == 1 && x != y){ // 回溯操作sz[y] -= sz[x]; fa[x] = x; for(int i = 1; i <= m; i ++) {iuy[y][i] -= iuy[x][i];}}
}int main(){scanf("%d%d", &n, &Q);init();m = (n - 1) / S + 1; // 块for(int i = 1; i <= n; i ++){scanf("%d", &w[i]); b[i] = w[i];}sort(b + 1, b + n + 1); // 离散化for(int i = 1; i <= n; i ++){w[i] = lower_bound(b + 1, b + n + 1, w[i]) - b;w[i] += number[w[i]] ++;num[w[i]] = i;iuy[i][(w[i] - 1) /	 S + 1] = 1;}for(int i = 1; i <= Q; i ++){int op, x, y; scanf("%d%d", &op, &x);if(op != 2) scanf("%d", &y), add(i - 1, i);if(op == 2) add(x, i);q[i] = {{x, y}, op}; // 离线}dfs(0);for(int i = 1; i <= Q; i ++){if(q[i].second == 3) printf("%d\n", ans[i]);}return 0;
}

块状链表

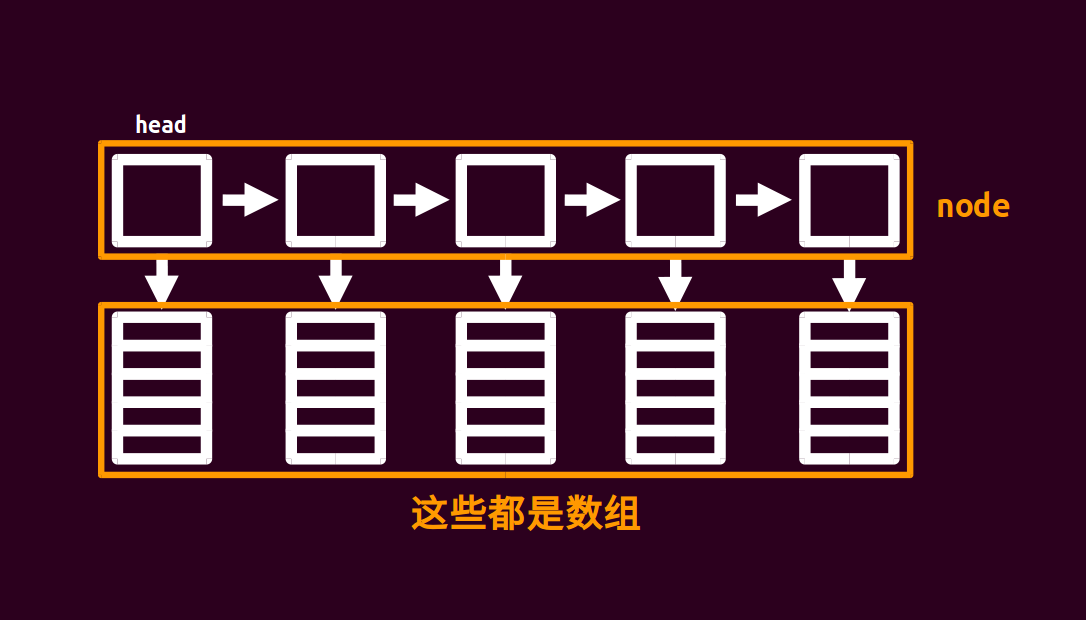
如上图（from oi-wiki），就是一个序列变成链表。

我们可以把原数组分成 $\sqrt n$ 个节点，每个节点挂一个长度为 $\sqrt n$ 的数组。

struct Node{char s[N + 20]; // 存的数组int len, pre, nxt; // 长度，前驱，后继
} p[M];

作为一个合格的块状链表，它应该至少支持：分裂、插入、查找三种操作。下面以 Luogu P4008 文本编辑器为例。

查找

单点（移动到某一个点 $k$ 后面）

我们可以一个节点一个节点的去找，每到一个节点后，判断是否要查找的第 $k$ 个数是否大于当前节点的大小。若大于，则将 $k$ 减去当前节点的大小；若小于等于，则在这块内寻找。时间复杂度 $\mathcal O(\sqrt n)$。

void Move(int k){x = 0;while(k > p[x].len) k -= p[x].len, x = p[x].nxt; // 一直往后跳y = k;
}

区间

和普通分块差不多，只需先单点找到左端点，再和普通分块一样跳就可以了。

void Get(int lenth){//左端点之前已经找到了if(p[x].len - y >= lenth){ // 节点内for(int i = y + 1; i <= y + lenth; i ++) putchar(p[x].s[i]);} else { // 节点间lenth -= p[x].len - y;for(int i = y + 1; i <= p[x].len; i ++) putchar(p[x].s[i]);int id = p[x].nxt;while(lenth > p[id].len){for(int i = 1; i <= p[id].len; i ++) putchar(p[id].s[i]);lenth -= p[id].len;id = p[id].nxt;}for(int i = 1; i <= lenth; i ++) putchar(p[id].s[i]);}puts("");
}

分裂

顾名思义，就是将一个节点从某处分成两个节点。我们只需要再开一个新的节点，将分裂出来的节点放到里面就可以了。

插入(在某个点后插入一段区间)

首先，我们要知道，在一个节点的内部是肯定是不可以插入一个节点的。所以，我们就需要先从插入节点的地方分裂开，再在这两个节点之间插入一段序列。

void Insert(int lenth){if(y < p[x].len){ // 如果在一个节点内部，分裂int nw = u.top(); u.pop(); // 从还未使用的节点中取出一个for(int j = y + 1; j <= p[x].len; j ++) p[nw].s[++ p[nw].len] = p[x].s[j]; // 先复制一份p[x].len = y;add(x, nw); // 增加分裂后的连边}int lst = x;for(int i = 1; i <= lenth;){ int nw = u.top(); u.pop();for(int j = 1; j <= N && i <= lenth; j ++, i ++) p[nw].s[++ p[nw].len] = str[i]; // 将插入的序列分好add(lst, nw); // 增加节点lst = nw;}
}

维护时间正确的关键：合并操作

如果一直按照上面的操作不断分裂，我们将无法保证块长稳定在 $\sqrt n$ 左右，进而时间复杂度骤增。因此，我们需要在每次分裂或者插入的时候，进行合并操作，将块长较小的（$\le \sqrt n$ 的）节点合并起来，以求时间复杂度的正确性。

void Merge(){int i = p[0].nxt;while(p[i].nxt){if(p[i].len + p[p[i].nxt].len <= N){ // 小于 $N = \sqrt n$if(x == p[i].nxt) x = i, y += p[i].len;for(int k = 1; k <= p[p[i].nxt].len; k ++) p[i].s[++ p[i].len] = p[p[i].nxt].s[k];u.push(p[i].nxt); del(p[i].nxt); }i = p[i].nxt;if(i == 0) break;}
}

Code

完整Code

#include<bits/stdc++.h>using namespace std;const int N = 2000, M = 2010;int x, y;
stack<int> u;
char str[2000010];struct Node{char s[N + 20];int len, pre, nxt;
} p[M];void Move(int k){x = 0;while(k > p[x].len) k -= p[x].len, x = p[x].nxt;y = k;
} void add(int a, int b){p[b].nxt = p[a].nxt, p[p[b].nxt].pre = b;p[a].nxt = b, p[b].pre = a;
}void del(int a){p[p[a].pre].nxt = p[a].nxt, p[p[a].nxt].pre = p[a].pre;p[a].nxt = p[a].len = p[a].pre = 0;
}void Insert(int lenth){if(y < p[x].len){int nw = u.top(); u.pop();for(int j = y + 1; j <= p[x].len; j ++) p[nw].s[++ p[nw].len] = p[x].s[j];p[x].len = y;add(x, nw);}int lst = x;for(int i = 1; i <= lenth;){int nw = u.top(); u.pop();for(int j = 1; j <= N && i <= lenth; j ++, i ++) p[nw].s[++ p[nw].len] = str[i];add(lst, nw);lst = nw;}
}void Merge(){int i = p[0].nxt;while(p[i].nxt){if(p[i].len + p[p[i].nxt].len <= N){if(x == p[i].nxt) x = i, y += p[i].len;for(int k = 1; k <= p[p[i].nxt].len; k ++) p[i].s[++ p[i].len] = p[p[i].nxt].s[k];u.push(p[i].nxt); del(p[i].nxt); }i = p[i].nxt;if(i == 0) break;}
} void Delete(int lenth){if(p[x].len - y >= lenth){for(int i = y + 1, j = y + lenth + 1; j <= p[x].len; i ++, j ++) p[x].s[i] = p[x].s[j];p[x].len -= lenth;} else {lenth -= p[x].len - y;p[x].len = y;int id = p[x].nxt;while(lenth > p[id].len){lenth -= p[id].len;u.push(id);id = p[id].nxt;del(p[id].pre);}for(int i = 1, j = lenth + 1; j <= p[id].len; i ++, j ++) p[id].s[i] = p[id].s[j];p[id].len -= lenth;}
}void Get(int lenth){if(p[x].len - y >= lenth){for(int i = y + 1; i <= y + lenth; i ++) putchar(p[x].s[i]);} else {lenth -= p[x].len - y;for(int i = y + 1; i <= p[x].len; i ++) putchar(p[x].s[i]);int id = p[x].nxt;while(lenth > p[id].len){for(int i = 1; i <= p[id].len; i ++) putchar(p[id].s[i]);lenth -= p[id].len;id = p[id].nxt;}for(int i = 1; i <= lenth; i ++) putchar(p[id].s[i]);}puts("");
}void Prev(){if(y == 1) y = p[x = p[x].pre].len;else y --;
}void Next(){if(y == p[x].len) y = 1, x = p[x].nxt;else y ++;
}int main(){for(int i = 2000; i; i --) u.push(i);int t; scanf("%d", &t);while(t --){int a; char op[10]; scanf("\n%s", op + 1);if(op[1] == 'I'){scanf("%d", &a);int n = a, i = 1;while(n){str[i] = getchar();if(str[i] >= 32 && str[i] <= 126) i ++, n --; }Insert(a);Merge();} else if(op[1] == 'D') {scanf("%d", &a);Delete(a);Merge();} else if(op[1] == 'M') {scanf("%d", &a);Move(a);} else if(op[1] == 'G') {scanf("%d", &a);Get(a);} else if(op[1] == 'P') Prev();else Next();}return 0;
}

STL中的块状链表：$rope$

$rope$ 是STL中的一种数据结构，头文件是 <ext/rope>，（好像不在万能头里）。使用时如下：

#include <ext/rope>
using namespace __gnu_cxx;

它支持块状链表的一般操作，但是实现方式是可持久化平衡树，所以时间复杂度只有 $\mathcal O(n log_n)$，远比 $\mathcal O(n \sqrt n)$ 小。

如下，给出一些基本操作：

操作	作用
`rope<int> a`	初始化一个 $rope$
`a.push_back(x)`	在 $a$ 的末尾插入一个数 $x$
`a.insert(pos, x, y)`	在位置 $pos$ 插入 $y$ （不写则默认为 $1$）个数 $x$
`a.erase(pos, x)`	在位置 $pos$ 删除 $x$ 个元素
`a.at(x)` 或 `a[x]`	访问 $a$ 的第 $x$ 个元素
`a.length()` 或 `a.size()`	获取 $a$ 的大小

需要注意的是，$rope$ 的下标由 $0$ 开始。

下面给出一个板子：
数论分块6

#include <bits/stdc++.h>
#include <ext/rope>using namespace std;
using namespace __gnu_cxx;rope<int> a;int main() {int t;scanf("%d", &t);for (int i = 1; i <= t; i++) {int x;scanf("%d", &x);a.push_back(x);}while (t--) {int op, l, r, c;scanf("%d%d%d%d", &op, &l, &r, &c);if (op == 0) {a.insert(l - 1, r);} else {printf("%d\n", a[r - 1]);}}return 0;
}

数论分块

题意：求 $\sum_{i = 1}^{n} \lfloor \frac{1}{n} \rfloor$，$n \le 10^{14}$

如果直接求，时间肯定会炸掉，那么，我们考虑优化。

如下图，是上面函数的图像，我们发现，原函数中，有很多的值是相同的。

因此，我们可以把这些相同的数合并在一起统计。

对于一个数 $i$，我们可以发现，他的右端点是 $\lfloor \frac{n}{\lfloor \frac{n}{i} \rfloor} \rfloor$。证明如下：

令 $k = \lfloor \frac{n}{i} \rfloor$，则一定有 $k \le \frac{n}{i}$。
那么，$i = \lfloor \frac{n}{k} \rfloor \ge \lfloor \frac{n}{\lfloor \frac{n}{i} \rfloor} \rfloor$，所以，$i$ 所在块的右端点为 $\lfloor \frac{n}{\lfloor \frac{n}{i} \rfloor} \rfloor$。

那么根据这一个东西我们就可以计算了。

时间复杂度

我们分块来看。

对于 $i \le \sqrt n$，我们可以发现，我们只需要遍历 $[1, \sqrt n]$；

对于 $i > \sqrt n$，他们的值域为 $[1, \sqrt n]$。

因此，总体的时间复杂度为 $\mathcal O(\sqrt n)$

Code

LL l = 1ll, r;
while(l <= n){r = n / (n / l);(ans -= 1ll * (r - l + 1ll) % Mod * (1ll * (n / l) % Mod) % Mod) %= Mod;(ans += Mod) %= Mod; l = r + 1ll;
}

例题 [Luogu P2261 余数和]

众所周知， $k \% i$ 可以表示成 $k - i \times \lfloor \frac{k}{i} \rfloor$。那么，原式 $= \sum_{i = 1} ^ {n} (k - i \times \lfloor \frac{k}{i} \rfloor) = \sum_{i = 1} ^ {n} k - \sum_{i = 1} ^ {n} i \times \lfloor \frac{k}{i} \rfloor$。

如此，我们就可以在 $\mathcal O(\sqrt n)$ 的时间复杂度内完成此题。

Code

#include<bits/stdc++.h>using namespace std;long long n, k;int main(){scanf("%lld%lld", &n, &k);long long l = 1, r, ans = n * k;while(l <= n){if(k / l == 0) r = n;else r = min(n, k / (k / l));ans -= (l + r) * (r - l + 1) / 2 * (k / l);l = r + 1;}printf("%lld\n", ans);return 0;
}

附录：对比线段树和分块的优缺点

对比角度	分块/块状链表	线段树
时间复杂度	$\mathcal O(n \sqrt n)$	$\mathcal O(n log_n)$
数据范围	$\le 10^5$	$\le 10^6$
代码复杂度	较简单	较难
可处理问题	区间加，乘，势能，插入/删除序列	区间加，乘，但不能插入/删除序列
思想难度	较难	适中

莫队

普通莫队

莫队算法可以解决一类离线区间询问问题，适用性极为广泛。

算法功能：

一个序列 $a_1, a_2, a_3, ..., a_n$ 中，查询区间 $[l, r]$ 的某种信息。把正常复杂度 $\mathcal O(n^2)$ 的算法优化成 $\mathcal O(n \sqrt{n})$ 。

主题思想

分块

把整个查询的序列离线下来之后，把整个序列分成 $\sqrt{n}$ 个块，每个块内在分别按查询的右端点排序 (节省时间)。

查询

用当前已有的 $[l, r]$ 序列，推出 $[l \pm 1, r \pm 1]$的信息，再根据需要查询的区间，加 / 删点。

时间复杂度分析

主要的复杂度由查询中，指针跳跃的时间。首先，左指针由于已经分好了块，最多跳 $\sqrt{n}$ 次，而右指针在每个块中最多最多可以跳 $n$ 次。总复杂度乘起来就是 $\mathcal O(n \sqrt{n})$ 。

注意事项 & 使用条件

整体的查询可以离线（分块用）。
需要可以由常数的复杂度由 $[l, r]$ ，推出 $[l \pm 1, r \pm 1]$。
时间复杂度允许 $\mathcal O(n \sqrt{n})$, ($2 \times 10^5$ 刚好可以卡过)。

例题——Luogu P3901 数列找不同

判断是否可以用莫队

复杂度 $10^5$，$\mathcal O(n\sqrt{n})$ 可过。
查询可以离线。
可以推出信息。

分块

离线下来直接分就可以了。

for(int i = 1; i <= m; i ++) b[i].l = read(), b[i].r = read(), b[i].id = i;//离线下来
sort(b + 1, b + m + 1, [](node a, node b)
{ return a.l / S != b.l / S ? a.l < b.l : a.r < b.r; }) ;//排序：不在一个块内的，按块排；在的，按右端点先后排

处理查询操作

考虑已知区间 $[l, r]$ 的信息，该如何推出下一个区间有多少个不同的值。那么，我们可以开一个桶，用来记录每个值在当前区间分别出现了多少次，那么将 $l$ 往左移时，只需要将对应的桶相应的加上一，如果加一以前没有记录过，就说明这是一个新增的值，需要把答案加一；把 $l$ 向右移时，则在桶中删除当前的值，如果桶中归零，那么相对应地，答案要减一。 $r$ 同理。

void add(int x){if(!t[a[x]]) tot ++;//以前的区间中没有出现过，更新答案t[a[x]] ++;
}void del(int x){if(t[a[x]] == 1) tot --;//删没了，要减一t[a[x]] --;
}

for(int i = 1, L = 1, R = 0; i <= m; i ++){while(L < b[i].l) del(L ++);//多了要删while(L > b[i].l) add(-- L);//少了要加while(R > b[i].r) del(R --);//多了要删while(R < b[i].r) add(++ R);//少了要加ans[b[i].id] = (tot == b[i].r - b[i].l + 1);//答案}

查看全文

http://www.njgz.com.cn/news/913.html

ACME协议

Microsoft SQL Server 2016 with SP3 GDR (2025 年 7 月更新)

网络流量中的旗帜狩猎：Wireshark CTF实战手册

day30

redis的过期时间算法为什么要使用最小堆来实现时间轮，为什么不使用一个循环数组作为核心数据结构(ds)

读心与芯：我们与机器人的无限未来07机器人的风险

多项式 - 生成函数

图灵奖和诺贝尔奖双料得主、AI教父Hinton：AI超越人类后，我们该怎么做

ICCV 2025 | 浙大等提出 SGCDet：自适应3D体素构建，重新定义多视图室内3D检测

国产GPU芯片的天花板来啦！打破一切质疑，现场4K全高画质流畅跑黑猴！！！

当AI教父都开始害怕AI

共生伙伴：2025人工智能十大趋势｜2025 WAIC报告重磅发布

数据泄露激增与防护策略详解

20250728

白话Docker系列（一）：用Web应用实例深入容器

用 Vite + Cloudflare Pages 实现模块级独立打包与部署的静态 CDN 分发

[07.27学习笔记] Tokenizer - Luna

STM32F103C8T6芯片介绍（下） - LI,Yi

GRUB 设置安全启动

【work记录】系统能力大赛数据库中的MVCC学习记录

FireStore如何查看空间占用情况？（未解决）

MIT6.s081_Lab8

关于同源策略和跨域请求

Codeforces Round 1039 (Div. 2) 1 ~ D

【转】[C#] 参数前加 in 的作用

循环链表实现的队列

操作	作用
`rope<int> a`	初始化一个 \(rope\)
`a.push_back(x)`	在 \(a\) 的末尾插入一个数 \(x\)
`a.insert(pos, x, y)`	在位置 \(pos\) 插入 \(y\) （不写则默认为 \(1\)）个数 \(x\)
`a.erase(pos, x)`	在位置 \(pos\) 删除 \(x\) 个元素
`a.at(x)` 或 `a[x]`	访问 \(a\) 的第 \(x\) 个元素
`a.length()` 或 `a.size()`	获取 \(a\) 的大小

对比角度	分块/块状链表	线段树
时间复杂度	\(\mathcal O(n \sqrt n)\)	\(\mathcal O(n log_n)\)
数据范围	\(\le 10^5\)	\(\le 10^6\)
代码复杂度	较简单	较难
可处理问题	区间加，乘，势能，插入/删除序列	区间加，乘，但不能插入/删除序列
思想难度	较难	适中

分块

分块思想

描述

时间复杂度

例题1 Luogu P3870 开关

题意

分块

例题2 Luogu P5064 等这场战争结束之后

分析

回滚

注意事项

Code

块状链表

查找

单点（移动到某一个点 \(k\) 后面）

区间

分裂

插入(在某个点后插入一段区间)

维护时间正确的关键：合并操作

Code

STL中的块状链表：\(rope\)

数论分块

题意：求 \(\sum_{i = 1}^{n} \lfloor \frac{1}{n} \rfloor\)，\(n \le 10^{14}\)

时间复杂度

Code

例题 [Luogu P2261 余数和]

附录：对比线段树和分块的优缺点

莫队

普通莫队

算法功能：

主题思想

分块

查询

时间复杂度分析

注意事项 & 使用条件

例题——Luogu P3901 数列找不同

判断是否可以用莫队

分块

处理查询操作

相关文章：