当前位置：首页 > news >正文

【leetcode刷题】动态规划 Part4 经典线性DP

news 2025/8/2 9:22:22

今天我们来回顾一下第四部分

直接看题

712:两个字符串的最小ASCLL删除和

给定两个字符串s1和s2，返回使两个字符串相等所需删除字符的ASCII值的最小和。

示例 1:

输入: s1 = "sea", s2 = "eat"
输出: 231
解释: 在 "sea" 中删除 "s" 并将 "s" 的值(115)加入总和。
在 "eat" 中删除 "t" 并将 116 加入总和。
结束时，两个字符串相等，115 + 116 = 231 就是符合条件的最小和。

示例 2:

输入: s1 = "delete", s2 = "leet"
输出: 403
解释: 在 "delete" 中删除 "dee" 字符串变成 "let"，
将 100[d]+101[e]+101[e] 加入总和。在 "leet" 中删除 "e" 将 101[e] 加入总和。
结束时，两个字符串都等于 "let"，结果即为 100+101+101+101 = 403 。
如果改为将两个字符串转换为 "lee" 或 "eet"，我们会得到 433 或 417 的结果，比答案更大。

提示:

0 <= s1.length, s2.length <= 1000
s1 和 s2 由小写英文字母组成

Solution

简单的题目，思路跟原版的LCS差不多

class Solution {
public:int minimumDeleteSum(string s1, string s2) {int l1=s1.length(),l2=s2.length();const int INF=1e9+7;vector<vector<int>>dp(l1+5,vector<int>(l2+5,INF));dp[0][0]=0;for(int i=1;i<=l1;i++) dp[i][0]=dp[i-1][0]+(s1[i-1]-'0'+48);for(int i=1;i<=l2;i++) dp[0][i]=dp[0][i-1]+(s2[i-1]-'0'+48);for(int i=1;i<=l1;i++){for(int j=1;j<=l2;j++){if(s1[i-1]==s2[j-1]) dp[i][j]=min(dp[i][j],dp[i-1][j-1]);dp[i][j]=min(dp[i][j],min(dp[i-1][j]+(s1[i-1]-'0'+48),dp[i][j-1]+s2[j-1]-'0'+48));}}return dp[l1][l2];}
};

72. 编辑距离

给你两个单词word1和word2，请返回将word1转换成word2所使用的最少操作数。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例 2：

输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

提示：

0 <= word1.length, word2.length <= 500
word1 和 word2 由小写英文字母组成

Solution

这道题啊....注意是因为可以删除，添加和替换的
所以我们的转移方程需要分类

class Solution {
public:int minDistance(string word1, string word2) {int l1=word1.length(),l2=word2.length();const int INF=1e9+7;vector<vector<int>>dp(l1+5,vector<int>(l2+5,INF));dp[0][0]=0;for(int i=1;i<=l1;i++) dp[i][0]=i;for(int i=1;i<=l2;i++) dp[0][i]=i;for(int i=1;i<=l1;i++){for(int j=1;j<=l2;j++){if(word1[i-1]==word2[j-1]) {dp[i][j]=min(dp[i][j],dp[i-1][j-1]);dp[i][j]=min(dp[i][j],min(dp[i-1][j],dp[i][j-1])+1);}dp[i][j]=min(dp[i][j],min(dp[i-1][j],min(dp[i][j-1],dp[i-1][j-1]))+1);}}return dp[l1][l2];}
};

1458. 两个子序列的最大点积

给你两个数组nums1和nums2。

请你返回nums1和nums2中两个长度相同的非空子序列的最大点积。

数组的非空子序列是通过删除原数组中某些元素（可能一个也不删除）后剩余数字组成的序列，但不能改变数字间相对顺序。比方说，[2,3,5] 是 [1,2,3,4,5] 的一个子序列而 [1,5,3] 不是。

示例 1：

输入：nums1 = [2,1,-2,5], nums2 = [3,0,-6]
输出：18
解释：从 nums1 中得到子序列 [2,-2] ，从 nums2 中得到子序列 [3,-6] 。
它们的点积为 (23 + (-2)(-6)) = 18 。

示例 2：

输入：nums1 = [3,-2], nums2 = [2,-6,7]
输出：21
解释：从 nums1 中得到子序列 [3] ，从 nums2 中得到子序列 [7] 。
它们的点积为 (3*7) = 21 。

示例 3：

输入：nums1 = [-1,-1], nums2 = [1,1]
输出：-1
解释：从 nums1 中得到子序列 [-1] ，从 nums2 中得到子序列 [1] 。
它们的点积为 -1 。

提示：

1 <= nums1.length, nums2.length <= 500
-1000 <= nums1[i], nums2[i] <= 100

Solution

我们这道题考虑用\(dp[i][j]\)表示nums1的前i个和nums2前j个的最大点积
然后直接用转移方程计算即可
注意：因为可以为空，所以可以用\(dp[i-1][j]\)转移，相当于在不足的地方补0

class Solution {
public:int maxDotProduct(vector<int>& nums1, vector<int>& nums2) {int l1=nums1.size(),l2=nums2.size();const int INF=1e9+7;vector<vector<int>>dp(l1+5,vector<int>(l2+5,-INF));dp[0][0]=0;for(int i=1;i<=l1;i++) dp[i][0]=0;for(int i=1;i<=l2;i++) dp[0][i]=0; for(int i=1;i<=l1;i++){for(int j=1;j<=l2;j++){dp[i][j]=max(dp[i][j],dp[i-1][j-1]+nums1[i-1]*nums2[j-1]);dp[i][j]=max(dp[i][j],max(dp[i-1][j],dp[i][j-1]));}}if(dp[l1][l2]!=0) return dp[l1][l2];int res=-INF;for(int i=0;i<=l1-1;i++){for(int j=0;j<=l2-1;j++){res=max(res,nums1[i]*nums2[j]);}}return res;}
};

718. 最长重复子数组

给两个整数数组nums1和nums2，返回两个数组中公共的、长度最长的子数组的长度。

示例 1：

输入：nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出：3
解释：长度最长的公共子数组是 [3,2,1] 。

示例 2：

输入：nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
输出：5

提示：

1 <= nums1.length, nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 100

Solution

子数组的题目道理都差不多，本题是把原题变为二维的而已

class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {int l1=nums1.size(),l2=nums2.size();const int INF=1e9+7;vector<vector<int>>dp(l1+5,vector<int>(l2+5,-INF));for(int i=1;i<=l1;i++){for(int j=1;j<=l2;j++){if(nums1[i-1]==nums2[j-1]){dp[i][j]=max(dp[i-1][j-1]+1,1);}}}int res=0;for(int i=1;i<=l1;i++){for(int j=1;j<=l2;j++){res=max(res,dp[i][j]);}}return res;}
};

115. 不同的子序列

给你两个字符串s和t，统计并返回在s的子序列中t出现的个数。

测试用例保证结果在32位有符号整数范围内。

示例 1：

输入：s = "rabbbit", t = "rabbit"
输出：3
解释：
如下所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
rabbbit
rabbbit
rabbbit

示例 2：

输入：s = "babgbag", t = "bag"
输出：5
解释：
如下所示, 有 5 种可以从 s 中得到 "bag" 的方案。
babgbag
babgbag
babgbag
babgbag
babgbag

提示：

1 <= s.length, t.length <= 1000
s 和 t 由英文字母组成

Solution

注意：这种写着结果是32位无符号整数的，通常过程中可能会出现爆int的情况
这道题我们用\(dp[i][j]\)表示前i个字符中，含有\(j\)个字符的方案数
然后转移方程就出来了

class Solution {
public:int numDistinct(string s, string t) {int l1=s.length(),l2=t.length();vector<vector<long long>>dp(l1+5,vector<long long>(l2+5,0));const int INF=(1<<31)-1;for(int i=0;i<=l1;i++) dp[i][0]=1;for(int i=1;i<=l1;i++){for(int j=1;j<=min(i,l2);j++){if(s[i-1]==t[j-1]){dp[i][j]+=dp[i-1][j-1]%INF;dp[i][j]%=INF;}dp[i][j]+=dp[i-1][j]%INF;}}return dp[l1][l2]%INF;}
};

3316. 从原字符串里进行删除操作的最多次数

给你一个长度为n的字符串source，一个字符串pattern且它是source 的子序列，和一个有序整数数组targetIndices，整数数组中的元素是 [0, n - 1] 中互不相同的数字。

定义一次操作为删除source中下标在idx的一个字符，且需要满足：

idx 是targetIndices中的一个元素。
删除字符后，pattern 仍然是source的一个子序列。

执行操作后不会改变字符在source中的下标位置。比方说，如果从 "acb" 中删除 'c' ，下标为 2 的字符仍然是 'b' 。

请你返回最多可以进行多少次删除操作。

子序列指的是在原字符串里删除若干个（也可以不删除）字符后，不改变顺序地连接剩余字符得到的字符串。

示例 1：

输入：source = "abbaa", pattern = "aba", targetIndices = [0,1,2]

输出：1

解释：

不能删除 source[0] ，但我们可以执行以下两个操作之一：

删除 source[1] ，source 变为 "a_baa" 。
删除 source[2] ，source 变为 "ab_aa" 。

示例 2：

输入：source = "bcda", pattern = "d", targetIndices = [0,3]

输出：2

解释：

进行两次操作，删除 source[0] 和 source[3] 。

示例 3：

输入：source = "dda", pattern = "dda", targetIndices = [0,1,2]

输出：0

解释：

不能在 source 中删除任何字符。

示例 4：

输入：source = "yeyeykyded", pattern = "yeyyd", targetIndices = [0,2,3,4]

输出：2

解释：

进行两次操作，删除 source[2] 和 source[3] 。

提示：

1 <= n == source.length <= 3 * 103
1 <= pattern.length <= n
1 <= targetIndices.length <= n
targetIndices 是一个升序数组。
输入保证 targetIndices 包含的元素在 [0, n - 1] 中且互不相同。
source 和 pattern 只包含小写英文字母。
输入保证 pattern 是 source 的一个子序列。

Solution

这道题的状态设计很有意思，我们考虑正难则反思想，要求出targetIndices中，source与pattern重合部分中最少的下标数
然后套一下LCS的公式，就可以了
还是需要想一想的

class Solution {
public:int maxRemovals(string source, string pattern, vector<int>& targetIndices) {int l1=source.length(),l2=pattern.length();int n=targetIndices.size();vector<bool>ma(l1+5,false);const int INF=1e9+7;vector<vector<int>>dp(l1+5,vector<int>(l2+5,INF));for(int i=0;i<=n-1;i++) ma[targetIndices[i]]=true;for(int i=0;i<=l1;i++) dp[i][0]=0;for(int i=1;i<=l1;i++){for(int j=1;j<=l2;j++){if(pattern[j-1]==source[i-1]){if(ma[i-1]){dp[i][j]=min(dp[i][j],dp[i-1][j]);dp[i][j]=min(dp[i][j],dp[i-1][j-1]+1);}else{dp[i][j]=min(dp[i][j],dp[i-1][j-1]);continue;}}else{dp[i][j]=min(dp[i-1][j],dp[i][j]);continue;}}}return n-dp[l1][l2];}
};

1639. 通过给定词典构造目标字符串的方案数

给你一个字符串列表words和一个目标字符串target。words中所有字符串都长度相同。

你的目标是使用给定的words字符串列表按照下述规则构造target：

从左到右依次构造target的每一个字符。
为了得到target第 i 个字符（下标从 0 开始），当 target[i] = words[j][k] 时，你可以使用words列表中第 j 个字符串的第 k 个字符。
一旦你使用了words中第 j 个字符串的第 k 个字符，你不能再使用words字符串列表中任意单词的第 x 个字符（x <= k）。也就是说，所有单词下标小于等于 k 的字符都不能再被使用。
请你重复此过程直到得到目标字符串target。

请注意，在构造目标字符串的过程中，你可以按照上述规定使用words列表中同一个字符串的多个字符。

请你返回使用words构造target的方案数。由于答案可能会很大，请对10^9 + 7取余后返回。

（译者注：此题目求的是有多少个不同的 k 序列，详情请见示例。）

示例 1：

输入：words = ["acca","bbbb","caca"], target = "aba"
输出：6
解释：总共有 6 种方法构造目标串。
"aba" -> 下标为 0 ("acca")，下标为 1 ("bbbb")，下标为 3 ("caca")
"aba" -> 下标为 0 ("acca")，下标为 2 ("bbbb")，下标为 3 ("caca")
"aba" -> 下标为 0 ("acca")，下标为 1 ("bbbb")，下标为 3 ("acca")
"aba" -> 下标为 0 ("acca")，下标为 2 ("bbbb")，下标为 3 ("acca")
"aba" -> 下标为 1 ("caca")，下标为 2 ("bbbb")，下标为 3 ("acca")
"aba" -> 下标为 1 ("caca")，下标为 2 ("bbbb")，下标为 3 ("caca")

示例 2：

输入：words = ["abba","baab"], target = "bab"
输出：4
解释：总共有 4 种不同形成 target 的方法。
"bab" -> 下标为 0 ("baab")，下标为 1 ("baab")，下标为 2 ("abba")
"bab" -> 下标为 0 ("baab")，下标为 1 ("baab")，下标为 3 ("baab")
"bab" -> 下标为 0 ("baab")，下标为 2 ("baab")，下标为 3 ("baab")
"bab" -> 下标为 1 ("abba")，下标为 2 ("baab")，下标为 3 ("baab")

示例 3：

输入：words = ["abcd"], target = "abcd"
输出：1

示例 4：

输入：words = ["abab","baba","abba","baab"], target = "abba"
输出：16

提示：

1 <= words.length <= 1000
1 <= words[i].length <= 1000
words 中所有单词长度相同。
1 <= target.length <= 1000
words[i] 和 target 都仅包含小写英文字母。

Solution

本质上还是两个序列的问题，我们需要使用构造方法，而且同一个words列之中如果不同行拥有同一个字母是算两个的
所以，这样我们就可以按照原来的思路来做，另外，为了降低时间复杂度，我们不可能逐个遍历words的全部行列，所以这时候的空间预处理就显得格外重要了。

class Solution {
public:int numWays(vector<string>& words, string target) {const int INF=1e9+7;int n=words.size();int l=words[0].size();int m=target.size();vector<vector<int>>dp(m+5,vector<int>(l+5,0));vector<vector<int>>ma(l+5,vector<int>(27,0));for(int i=0;i<=n-1;i++){for(int j=0;j<=l-1;j++){ma[j][words[i][j]-'a'+1]++;}}for(int i=0;i<=l;i++) dp[0][i]=1;for(int i=1;i<=m;i++){for(int j=1;j<=l;j++){dp[i][j]=dp[i][j-1]%INF;dp[i][j]+=(long long)dp[i-1][j-1]*(long long)ma[j-1][target[i-1]-'a'+1]%INF;dp[i][j]%=INF;}}return dp[m][l]%INF;}
};

97. 交错字符串

给定三个字符串 s1、s2、s3，请你帮忙验证 s3 是否是由 s1 和 s2 交错组成的。

两个字符串 s 和 t 交错的定义与过程如下，其中每个字符串都会被分割成若干非空子字符串：

s = s1 + s2 + ... + sn
t = t1 + t2 + ... + tm
|n - m| <= 1
交错是 s1 + t1 + s2 + t2 + s3 + t3 + ... 或者 t1 + s1 + t2 + s2 + t3 + s3 + ...

注意：a + b 意味着字符串 a 和 b 连接。

示例 1：

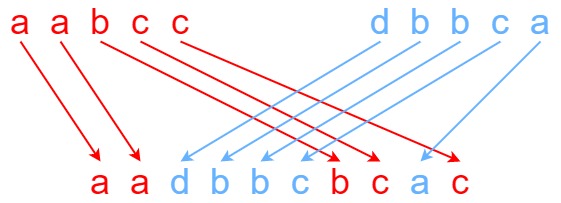
输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
输出：true

示例 2：

输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
输出：false

示例 3：

输入：s1 = "", s2 = "", s3 = ""
输出：true

提示：

0 <= s1.length, s2.length <= 100
0 <= s3.length <= 200
s1、s2、和 s3 都由小写英文字母组成

Solution

为了剪枝，首先我们肯定要看这个字符串的长度是否跟原来两个字符串拼起来相等
用\(dp[i][j]\)表示s1的前\(i\)项与s2的前\(j\)项能否拼成s3的前\(i+j\)项
然后转移方程就出来了

class Solution {
public:bool isInterleave(string s1, string s2, string s3) {int l1=s1.length(),l2=s2.length();int l3=s3.length();if(l3!=l1+l2) return false;vector<vector<bool>>dp(l1+5,vector<bool>(l2+5,false));dp[0][0]=true;for(int i=1;i<=l1;i++){bool temp=s1[i-1]==s3[i-1];dp[i][0]=dp[i-1][0]&temp;}for(int i=1;i<=l2;i++){bool temp=s2[i-1]==s3[i-1];dp[0][i]=dp[0][i-1]&temp;}for(int i=1;i<=l1;i++){for(int j=1;j<=l2;j++){if(s1[i-1]==s3[i+j-1]) dp[i][j]=dp[i][j]|dp[i-1][j];if(s2[j-1]==s3[i+j-1]) dp[i][j]=dp[i][j]|dp[i][j-1];}}return dp[l1][l2];}
};

44. 通配符匹配

给你一个输入字符串 (s) 和一个字符模式 (p) ，请你实现一个支持 '?' 和 '*' 匹配规则的通配符匹配：

'?' 可以匹配任何单个字符。
``'*'` 可以匹配任意字符序列（包括空字符序列）。

判定匹配成功的充要条件是：字符模式必须能够 完全匹配 输入字符串（而不是部分匹配）。

示例 1：

输入：s = "aa", p = "a"
输出：false
解释："a" 无法匹配 "aa" 整个字符串。

示例 2：

输入：s = "aa", p = ""
输出：true
解释：'' 可以匹配任意字符串。

示例 3：

输入：s = "cb", p = "?a"
输出：false
解释：'?' 可以匹配 'c', 但第二个 'a' 无法匹配 'b'。

提示：

0 <= s.length, p.length <= 2000
s仅由小写英文字母组成
p仅由小写英文字母、'?' 或 '*' 组成

Solution

算是比较难的题，当然，问号其实不难，难的是星号
我们来想一想，我们把s的前\(i\)项与p的前\(j\)项能否匹配设为\(dp[i][j]\)
那么，星号的推出只有两种情况，一种是用了多处，另一种是一个也不用
用了多处，可以理解为多个地方都表示了，这里到底是用还是不用
于是就化归为，这一处到底用不用星号的问题（因为有循环顺序存在）
转移方程就出来了，注意初始化

class Solution {
public:bool isMatch(string s, string p) {int l1=s.length(),l2=p.length();vector<vector<bool>>dp(l1+5,vector<bool>(l2+5,false));dp[0][0]=true;for(int i=1;i<=l2;i++){if(p[i-1]!='*') break;dp[0][i]=true;}for(int i=1;i<=l1;i++){for(int j=1;j<=l2;j++){if(p[j-1]=='?'){dp[i][j]=dp[i][j]|dp[i-1][j-1];continue;}if(p[j-1]=='*'){dp[i][j]=dp[i][j]|dp[i][j-1];dp[i][j]=dp[i][j]|dp[i-1][j];continue;}if(s[i-1]==p[j-1]) dp[i][j]=dp[i][j]|dp[i-1][j-1];}}return dp[l1][l2];}
};

10. 正则表达式匹配

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素

所谓匹配，是要涵盖 整个 字符串 s 的，而不是部分字符串。

示例 1：

输入：s = "aa", p = "a"
输出：false
解释："a" 无法匹配 "aa" 整个字符串。

示例 2:

输入：s = "aa", p = "a"
输出：true
解释：因为 '' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

示例 3：

输入：s = "ab", p = "."
输出：true
解释："." 表示可匹配零个或多个（'*'）任意字符（'.'）。

提示：

1 <= s.length <= 20
1 <= p.length <= 20
s 只包含从 a-z 的小写字母。
p 只包含从 a-z 的小写字母，以及字符 . 和 *。
保证每次出现字符 * 时，前面都匹配到有效的字符

Solution

因为我们还没学过python的正则表达式匹配，所以要知道一点：C*也可以代表空的
思路跟前面那题有点像，但是要考虑的是，这个符号前面是什么符号，以及它们之间的转移方程关系

class Solution {
public:bool isMatch(string s, string p) {int l1=s.length(),l2=p.length();vector<vector<bool>>dp(l1+5,vector<bool>(l2+5,false));dp[0][0]=true;int temp=0;int las=1;for(int i=1;i<=l2;i++){if(p[i-1]!='*') temp++;if(temp>=2) break;if(p[i-1]=='*'){dp[0][i]=true;temp=0;las=i+1;}}for(int i=1;i<=l1;i++){for(int j=1;j<=l2;j++){if(p[j-1]=='.'){dp[i][j]=dp[i-1][j-1]|dp[i][j];continue;}if(p[j-1]=='*'){dp[i][j]=dp[i][j]|dp[i][j-2];if(p[j-2]=='.'){dp[i][j]=dp[i][j]|dp[i-1][j];dp[i][j]=dp[i][j]|dp[i][j-1];}if(p[j-2]==s[i-1]){dp[i][j]=dp[i][j]|dp[i-1][j];dp[i][j]=dp[i][j]|dp[i][j-1];}if(p[j-2]=='*'){dp[i][j]=dp[i][j-1]|dp[i][j];}continue;}if(s[i-1]==p[j-1]) dp[i][j]=dp[i-1][j-1]|dp[i][j];}}for(int i=0;i<=l2;i++){for(int j=0;j<=l1;j++){cout<<dp[j][i]<<' ';}cout<<endl;}return dp[l1][l2];}
};

1964. 找出到每个位置为止最长的有效障碍赛跑路线

你打算构建一些障碍赛跑路线。给你一个 下标从 0 开始的整数数组 obstacles，数组长度为n，其中obstacles[i]表示第 i 个障碍的高度。

对于每个介于 0 和 n - 1 之间（包含 0 和 n - 1）的下标 i ，在满足下述条件的前提下，请你找出 obstacles 能构成的最长障碍路线的长度：

你可以选择下标介于 0 到 i 之间（包含 0 和 i）的任意个障碍。
在这条路线中，必须包含第 i 个障碍。
你必须按障碍在 obstacles 中的 出现顺序 布置这些障碍。
除第一个障碍外，路线中每个障碍的高度都必须和前一个障碍相同或者更高。

返回长度为 n 的答案数组 ans ，其中 ans[i] 是上面所述的下标 i 对应的最长障碍赛跑路线的长度。

示例 1：

输入：obstacles = [1,2,3,2]
输出：[1,2,3,3]
解释：每个位置的最长有效障碍路线是：

i = 0: [1], [1] 长度为 1
i = 1: [1,2], [1,2] 长度为 2
i = 2: [1,2,3], [1,2,3] 长度为 3
i = 3: [1,2,3,2], [1,2,2] 长度为 3

示例 2：

输入：obstacles = [2,2,1]
输出：[1,2,1]
解释：每个位置的最长有效障碍路线是：

i = 0: [2], [2] 长度为 1
i = 1: [2,2], [2,2] 长度为 2
i = 2: [2,2,1], [1] 长度为 1

示例 3：

输入：obstacles = [3,1,5,6,4,2]
输出：[1,1,2,3,2,2]
解释：每个位置的最长有效障碍路线是：

i = 0: [3], [3] 长度为 1
i = 1: [3,1], [1] 长度为 1
i = 2: [3,1,5], [3,5] 长度为 2, [1,5] 也是有效的障碍赛跑路线
i = 3: [3,1,5,6], [3,5,6] 长度为 3, [1,5,6] 也是有效的障碍赛跑路线
i = 4: [3,1,5,6,4], [3,4] 长度为 2, [1,4] 也是有效的障碍赛跑路线
i = 5: [3,1,5,6,4,2], [1,2] 长度为 2

提示：

n == obstacles.length
1 <= n <= 10^5
1 <= obstacles[i] <= 10^7

Solution

人话：二分法求以每个元素结尾的最长不下降子序列长度
多一个DP数组就可以了

class Solution {
public:vector<int> longestObstacleCourseAtEachPosition(vector<int>& obstacles) {int n=obstacles.size();vector<int>dp(n,0);int fdp[n+5];for(int i=1;i<=n;i++) fdp[i]=0;fdp[1]=obstacles[0];dp[0]=1;int len=1;for(int i=1;i<=n-1;i++){if(obstacles[i]>=fdp[len]){fdp[++len]=obstacles[i]; dp[i]=max(dp[i],len);continue;}int x=upper_bound(fdp+1,fdp+1+len,obstacles[i])-fdp;fdp[x]=min(fdp[x],obstacles[i]);dp[i]=max(dp[i],x);}   return dp;}
};

2111. 使数组 K 递增的最少操作次数

给你一个下标从 0 开始包含 n 个正整数的数组 arr ，和一个正整数 k 。

如果对于每个满足 k <= i <= n-1 的下标 i ，都有 arr[i-k] <= arr[i] ，那么我们称 arr 是 K 递增 的。

比方说，arr = [4, 1, 5, 2, 6, 2] 对于 k = 2 是 K 递增的，因为：
- arr[0] <= arr[2] (4 <= 5)
- arr[1] <= arr[3] (1 <= 2)
- arr[2] <= arr[4] (5 <= 6)
- arr[3] <= arr[5] (2 <= 2)
但是，相同的数组 arr 对于 k = 1 不是 K 递增的（因为 arr[0] > arr[1]），对于 k = 3 也不是 K 递增的（因为 arr[0] > arr[3] ）。

每一次 操作 中，你可以选择一个下标 i 并将 arr[i] 改成任意 正整数。

请你返回对于给定的 k ，使数组变成 K 递增的 最少操作次数 。

示例 1：

输入：arr = [5,4,3,2,1], k = 1
输出：4
解释：
对于 k = 1 ，数组最终必须变成非递减的。
可行的 K 递增结果数组为 [5,6,7,8,9]，[1,1,1,1,1]，[2,2,3,4,4] 。它们都需要 4 次操作。
次优解是将数组变成比方说 [6,7,8,9,10] ，因为需要 5 次操作。
显然我们无法使用少于 4 次操作将数组变成 K 递增的。

示例 2：

输入：arr = [4,1,5,2,6,2], k = 2
输出：0
解释：
这是题目描述中的例子。
对于每个满足 2 <= i <= 5 的下标 i ，有 arr[i-2] <= arr[i] 。
由于给定数组已经是 K 递增的，我们不需要进行任何操作。

示例 3：

输入：arr = [4,1,5,2,6,2], k = 3
输出：2
解释：
下标 3 和 5 是仅有的 3 <= i <= 5 且不满足 arr[i-3] <= arr[i] 的下标。
将数组变成 K 递增的方法之一是将 arr[3] 变为 4 ，且将 arr[5] 变成 5 。
数组变为 [4,1,5,4,6,5] 。
可能有其他方法将数组变为 K 递增的，但没有任何一种方法需要的操作次数小于 2 次。

提示：

1 <= arr.length <= 10^5
1 <= arr[i], k <= arr.length

Solution

人话：同余的最长不下降子序列

class Solution {
public:int kIncreasing(vector<int>& arr, int k) {int n=arr.size();vector<vector<int>>ma(k+5);for(int i=0;i<=k-1;i++){for(int j=i;j<=n-1;j+=k) ma[i].push_back(arr[j]);}vector<int>dp;int ans=0;for(int i=0;i<=k-1;i++){int len=1;dp.push_back(0);dp.push_back(ma[i][0]);for(int j=1;j<=ma[i].size()-1;j++){if(ma[i][j]>=dp[len]){dp.push_back(ma[i][j]);len++;continue;}int x=upper_bound(dp.begin(),dp.end(),ma[i][j])-dp.begin();dp[x]=min(dp[x],ma[i][j]);}   ans+=ma[i].size()-len;dp.clear();}return ans;}
};

354. 俄罗斯套娃信封问题

给你一个二维整数数组 envelopes ，其中 envelopes[i] = [wi, hi]，表示第 i 个信封的宽度和高度。

当另一个信封的宽度和高度都比这个信封大的时候，这个信封就可以放进另一个信封里，如同俄罗斯套娃一样。

请计算 最多能有多少个 信封能组成一组“俄罗斯套娃”信封（即可以把一个信封放到另一个信封里面）。

注意：不允许旋转信封。

示例 1：

输入：envelopes = [ [5,4],[6,4],[6,7],[2,3] ]
输出：3
解释：最多信封的个数为 3, 组合为: [2,3] => [5,4] => [6,7]。

示例 2：

输入：envelopes = [ [1,1],[1,1],[1,1] ]
输出：1

提示：

1 <= envelopes.length <= 10^5
envelopes[i].length == 2
1 <= wi, hi <= 10^5

Solution

化多维为单维，第一个要想的就是，我要怎么固定一个维度
也就是所谓的冻结
在本题中，我们要考虑的就是固定第一个维度，这很容易，就是我们要对第一维进行排序
那么，怎么让第一维相等的序列不会干扰我们求二维LIS呢？小窍门：就是对第二维进行降序排列，然后在遍历的时候，第一维相等的元素就不会被错误选入。

class Solution {
public:int maxEnvelopes(vector<vector<int>>& envelopes) {int n=envelopes.size();sort(envelopes.begin(),envelopes.end(),[](const vector<int> &x,const vector<int> &y){ if(x[0]==y[0]) return x[1]>y[1]; else return x[0]<y[0];});vector<int>dp;dp.push_back(0);dp.push_back(envelopes[0][1]);int len=1;for(int i=1;i<=n-1;i++){if(envelopes[i][1]>dp[len]){len++;dp.push_back(envelopes[i][1]);continue;}int x=lower_bound(dp.begin(),dp.end(),envelopes[i][1])-dp.begin();dp[x]=min(dp[x],envelopes[i][1]);}return len;}
};

1691. 堆叠长方体的最大高度

给你 n 个长方体 cuboids ，其中第 i 个长方体的长宽高表示为 cuboids[i] = [widthi, lengthi, heighti]（下标从 0 开始）。请你从 cuboids 选出一个 子集 ，并将它们堆叠起来。

如果 width_i <= width_j 且 length_i <= length_j 且 height_i <= height_j ，你就可以将长方体 i 堆叠在长方体 j 上。你可以通过旋转把长方体的长宽高重新排列，以将它放在另一个长方体上。

返回 堆叠长方体 cuboids 可以得到的 最大高度 。

示例 1：

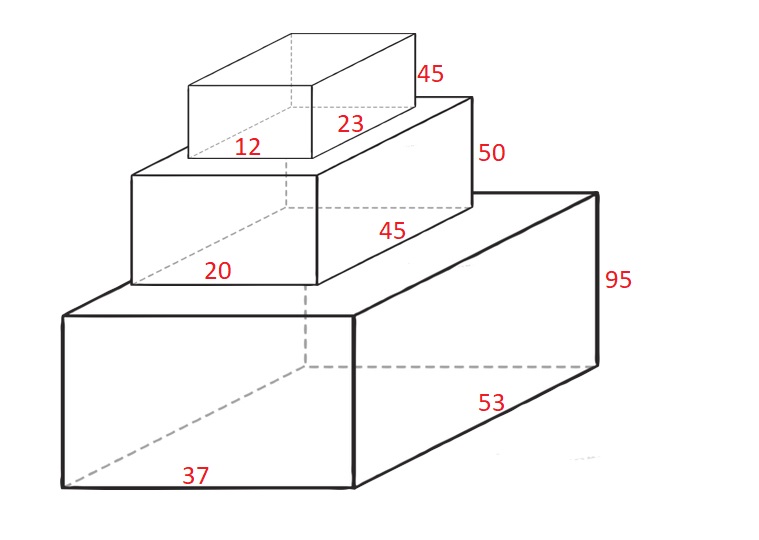
输入：cuboids = [ [50,45,20],[95,37,53],[45,23,12] ]
输出：190
解释：
第 1 个长方体放在底部，53x37 的一面朝下，高度为 95 。
第 0 个长方体放在中间，45x20 的一面朝下，高度为 50 。
第 2 个长方体放在上面，23x12 的一面朝下，高度为 45 。
总高度是 95 + 50 + 45 = 190 。

示例 2：

输入：cuboids = [ [38,25,45],[76,35,3] ]
输出：76
解释：
无法将任何长方体放在另一个上面。
选择第 1 个长方体然后旋转它，使 35x3 的一面朝下，其高度为 76 。

示例 3：

输入：cuboids = [ [7,11,17],[7,17,11],[11,7,17],[11,17,7],[17,7,11],[17,11,7] ]
输出：102
解释：
重新排列长方体后，可以看到所有长方体的尺寸都相同。
你可以把 11x7 的一面朝下，这样它们的高度就是 17 。
堆叠长方体的最大高度为 6 * 17 = 102 。

提示：

n == cuboids.length
1 <= n <= 100
1 <= width_i, length_i, height_i <= 100

Solution

跟上题其实是有点像的，我们会从样例发现，对于已经排好序的三个元素组而言，必须满足每个元素都要大于对应元素，而不是田忌赛马。
所以，高度自然就通过旋转选择最高的那个，至于排序，这道题应该按照正序排，毕竟我们需要的还是高度，而且这道题也不卡什么等号的问题，我们这么排只需要在遍历的时候验证一下就可以了

class Solution {
public:int maxHeight(vector<vector<int>>& cuboids) {int n=cuboids.size();for(int i=0;i<=n-1;i++){sort(cuboids[i].begin(),cuboids[i].end(),[](const int &x,const int &y){ return x>=y; });}sort(cuboids.begin(),cuboids.end(),[](const vector<int> &x,const vector<int> &y){ if(x[0]==y[0]){ if(x[1]==y[1]) return x[2]<y[2]; else return x[1]<y[1];} else return x[0]<y[0];});vector<int>dp(n+5,0);dp[0]=cuboids[0][0];for(int i=0;i<=n-1;i++){for(int j=0;j<=i-1;j++){if(cuboids[j][0]<=cuboids[i][0]&&cuboids[j][1]<=cuboids[i][1]&&cuboids[j][2]<=cuboids[i][2]){dp[i]=max(dp[i],dp[j]+cuboids[i][0]);continue;}else dp[i]=max(dp[i],cuboids[i][0]);}}int ans=0;for(int i=0;i<=n-1;i++) ans=max(ans,dp[i]);return ans;}
};

2407. 最长递增子序列 II

给你一个整数数组 nums 和一个整数 k 。

找到 nums 中满足以下要求的最长子序列：

子序列 严格递增
子序列中相邻元素的差值 不超过 k 。

请你返回满足上述要求的 最长子序列 的长度。

子序列 是从一个数组中删除部分元素后，剩余元素不改变顺序得到的数组。

示例 1：

输入：nums = [4,2,1,4,3,4,5,8,15], k = 3
输出：5
解释：
满足要求的最长子序列是 [1,3,4,5,8] 。
子序列长度为 5 ，所以我们返回 5 。
注意子序列 [1,3,4,5,8,15] 不满足要求，因为 15 - 8 = 7 大于 3 。

示例 2：

输入：nums = [7,4,5,1,8,12,4,7], k = 5
输出：4
解释：
满足要求的最长子序列是 [4,5,8,12] 。
子序列长度为 4 ，所以我们返回 4 。

示例 3：

输入：nums = [1,5], k = 1
输出：1
解释：
满足要求的最长子序列是 [1] 。
子序列长度为 1 ，所以我们返回 1 。

提示：

1 <= nums.length <= 10^5
1 <= nums[i], k <= 10^5

Solution

这题是重头戏了，我们要介绍一种新的优化LIS的方法，也就是线段树优化
回顾之前我们写的转移方程，\(f[i]=max(f[j]+1,1),nums[i]>nums[j]\)
那么，我们考虑到对于对于一个元素，当其他元素比它小的时候，取其中最大的将其转移，这是不是很像线段树？
我们令dp[i]表示nums[i]为结尾的最长递增子序列长度，然后构建线段树，每次转移相当于更新线段树上的值

class Solution {
public:struct SegmentTree{int l,r,ma;};void build(SegmentTree tree[],int x,int l,int r){tree[x].l=l;tree[x].r=r;if(tree[x].l==tree[x].r){tree[x].ma=0;return ;}int mid=(tree[x].l+tree[x].r)>>1;build(tree,x<<1,l,mid);build(tree,(x<<1)+1,mid+1,r); tree[x].ma=max(tree[x<<1].ma,tree[(x<<1)+1].ma);return ;}void change(SegmentTree tree[],int x,int n,int k){if(tree[x].l==tree[x].r){tree[x].ma=k;return ;}int mid=(tree[x].l+tree[x].r)>>1;if(n<=mid) change(tree,x<<1,n,k);else change(tree,(x<<1)+1,n,k);tree[x].ma=max(tree[x<<1].ma,tree[(x<<1)+1].ma);return ;}int query(SegmentTree tree[],int x,int l,int r){if(l<=tree[x].l&&tree[x].r<=r) return tree[x].ma;int mid=(tree[x].l+tree[x].r)>>1;int ans=0;if(l<=mid) ans=max(ans,query(tree,x<<1,l,r));if(r>mid) ans=max(ans,query(tree,(x<<1)+1,l,r));return ans; }int lengthOfLIS(vector<int>& nums, int k) {int n=nums.size();      int maxx=0;for(int num:nums) maxx=max(maxx,num);SegmentTree tree[4*maxx];build(tree,1,1,maxx);for(int i=0;i<=n-1;i++){int temp=0;if(nums[i]==1){change(tree,1,nums[i],1);continue;}if(nums[i]>k) temp=query(tree,1,nums[i]-k,nums[i]-1);else temp=query(tree,1,1,nums[i]-1);change(tree,1,nums[i],temp+1);}int ans=query(tree,1,1,maxx);return ans;}
};

1187. 使数组严格递增

给你两个整数数组 arr1 和 arr2，返回使 arr1 严格递增所需要的最小「操作」数（可能为 0）。

每一步「操作」中，你可以分别从 arr1 和 arr2 中各选出一个索引，分别为 i 和 j，0 <= i <= arr1.length 和 0 <= j <= arr2.length，然后进行赋值运算 arr1[i] = arr2[j]。

如果无法让 arr1 严格递增，请返回 -1。

示例 1：

输入：arr1 = [1,5,3,6,7], arr2 = [1,3,2,4]
输出：1
解释：用 2 来替换 5，之后 arr1 = [1, 2, 3, 6, 7]。

示例 2：

输入：arr1 = [1,5,3,6,7], arr2 = [4,3,1]
输出：2
解释：用 3 来替换 5，然后用 4 来替换 3，得到 arr1 = [1, 3, 4, 6, 7]。

示例 3：

输入：arr1 = [1,5,3,6,7], arr2 = [1,6,3,3]
输出：-1
解释：无法使 arr1 严格递增。

提示：

1 <= arr1.length, arr2.length <= 2000
0 <= arr1[i], arr2[i] <= 10^9

Solution

这道题其实是卡在了状态设计，事实上，当我们对一个题目一筹莫展的时候，多半要怀疑是不是状态设计错了
我们用\(dp[i][j]\)表示前\(i\)个元素被调换了\(j\)次的最小值，根据贪心的原理，我们肯定要选择比它大，而且最小的那一个，这就是二分查找的应用了

class Solution {
public:int makeArrayIncreasing(vector<int>& arr1, vector<int>& arr2) {int n=arr1.size(),m=arr2.size();sort(arr2.begin(),arr2.end());const int INF=1e9+7;vector<vector<int>>dp(n+5,vector<int>(n+5,INF));dp[0][0]=arr1[0];dp[0][1]=arr2[0];for(int i=1;i<=n-1;i++){for(int j=0;j<=i+1;j++){if(j==0){if(arr1[i]>dp[i-1][0]) dp[i][0]=arr1[i];continue;}if(dp[i-1][j-1]!=INF){auto z=upper_bound(arr2.begin(),arr2.end(),dp[i-1][j-1]);if(z!=arr2.end()) dp[i][j]=min(dp[i][j],*z);}if(dp[i-1][j]!=INF){if(arr1[i]>dp[i-1][j]) dp[i][j]=min(dp[i][j],arr1[i]);}}}int ans=-1;for(int i=0;i<=n;i++){if(dp[n-1][i]!=INF){ans=i;break;}}return ans;}
};

1713. 得到子序列的最少操作次数

给你一个数组 target ，包含若干 互不相同 的整数，以及另一个整数数组arr ，arr 可能包含重复元素。

每一次操作中，你可以在 arr 的任意位置插入任一整数。比方说，如果 arr = [1,4,1,2] ，那么你可以在中间添加 3 得到 [1,4,3,1,2] 。你可以在数组最开始或最后面添加整数。

请你返回最少操作次数，使得 target 成为 arr 的一个子序列。

一个数组的 子序列 指的是删除原数组的某些元素（可能一个元素都不删除），同时不改变其余元素的相对顺序得到的数组。比方说，[2,7,4] 是 [4,2,3,7,2,1,4] 的子序列（加粗元素），但 [2,4,2] 不是子序列。

示例 1：

输入：target = [5,1,3], arr = [9,4,2,3,4]
输出：2
解释：你可以添加 5 和 1 ，使得 arr 变为 [5,9,4,1,2,3,4] ，target 为 arr 的子序列。

示例 2：

输入：target = [6,4,8,1,3,2], arr = [4,7,6,2,3,8,6,1]
输出：3

提示：

1 <= target.length, arr.length <= 105
1 <= target[i], arr[i] <= 109
target 不包含任何重复元素。#

Solution

LIS求LCS的题，不解释了

class Solution {
public:int minOperations(vector<int>& target, vector<int>& arr) {int n=target.size(),m=arr.size();const int INF=1e9+7;map<int,int>ma;for(int i=0;i<=n-1;i++){ma[target[i]]=i+1;}int len=0;vector<int>dp;dp.push_back(0);for(int i=0;i<=m-1;i++){if(ma.find(arr[i])==ma.end()) continue;if(ma[arr[i]]>dp[len]){ dp.push_back(ma[arr[i]]);len++;continue;}int x=lower_bound(dp.begin(),dp.end(),ma[arr[i]])-dp.begin();dp[x]=min(dp[x],ma[arr[i]]);}return n-len;}
};

3288. 最长上升路径的长度

给你一个长度为 n 的二维整数数组 coordinates 和一个整数 k ，其中 0 <= k < n 。

coordinates[i] = [xi, yi] 表示二维平面里一个点 (xi, yi) 。

如果一个点序列 (x1, y1), (x2, y2), (x3, y3), ..., (xm, ym) 满足以下条件，那么我们称它是一个长度为 m 的 上升序列 ：

对于所有满足 1 <= i < m 的 i 都有 ``xi < xi + 1 且 yi < yi + 1 。
对于所有 1 <= i <= m 的 i 对应的点 (xi, yi) 都在给定的坐标数组里。

请你返回包含坐标 coordinates[k] 的 最长上升路径 的长度。

示例 1：

输入：coordinates = [ [3,1],[2,2],[4,1],[0,0],[5,3] ], k = 1

输出：3

解释：

(0, 0) ，(2, 2) ，(5, 3) 是包含坐标 (2, 2) 的最长上升路径。

示例 2：

输入：coordinates = [ [2,1],[7,0],[5,6] ], k = 2

输出：2

解释：

(2, 1) ，(5, 6) 是包含坐标 (5, 6) 的最长上升路径。

提示：

1 <= n == coordinates.length <= 10^5
coordinates[i].length == 2
0 <= coordinates[i][0], coordinates[i][1] <= 10^9
coordinates 中的元素 互不相同 。
0 <= k <= n - 1

Solution

其实看到一定要包含这个条件，我们就能想到把原式断成前后两片，分别求出最长递增子序列和最长递减子序列（用取负数求最长递增子序列的方法）求出，然后加起来
二分法求每个数对应结尾的最长递增子序列长度前面已经介绍过了，这里不再赘述

class Solution {
public:int maxPathLength(vector<vector<int>>& coordinates, int k) {int n=coordinates.size();const int INF=1e9+7;struct node{int x,y,id;bool operator<(const node &other){if(x==other.x) return y>other.y;return x<other.x;}};node ma[n+5];for(int i=0;i<=n-1;i++){ma[i+1].x=coordinates[i][0],ma[i+1].y=coordinates[i][1];ma[i+1].id=i+1;}sort(ma+1,ma+1+n);int res=0;for(int i=1;i<=n;i++){if(ma[i].id==k+1){res=i;break;}}vector<int>dp;vector<int>fdp(n+5,0);int len=1;dp.push_back(-1);dp.push_back(ma[1].y);fdp[1]=1;for(int i=2;i<=res;i++){if(ma[i].y>dp[len]){dp.push_back(ma[i].y);len++;fdp[i]=max(fdp[i],len);continue;}int x=lower_bound(dp.begin(),dp.end(),ma[i].y)-dp.begin();fdp[i]=x;dp[x]=min(dp[x],ma[i].y);}int tem1=max(fdp[res],1);if(res==1) tem1=1;dp.clear();for(int i=0;i<=n+4;i++) fdp[i]=0;dp.push_back(-INF);dp.push_back(-ma[n].y);len=1;fdp[n]=1;for(int i=n-1;i>=res;i--){if(-ma[i].y>dp[len]){len++;dp.push_back(-ma[i].y);fdp[i]=len;continue;}int x=lower_bound(dp.begin(),dp.end(),-ma[i].y)-dp.begin();fdp[i]=x;dp[x]=min(-ma[i].y,dp[x]);}int tem2=max(fdp[res],1);return tem1+tem2-1;}
};

368. 最大整除子集

给你一个由 无重复 正整数组成的集合 nums ，请你找出并返回其中最大的整除子集 answer ，子集中每一元素对 (answer[i], answer[j]) 都应当满足：

answer[i] % answer[j] == 0 ，或
answer[j] % answer[i] == 0

如果存在多个有效解子集，返回其中任何一个均可。

示例 1：

输入：nums = [1,2,3]
输出：[1,2]
解释：[1,3] 也会被视为正确答案。

示例 2：

输入：nums = [1,2,4,8]
输出：[1,2,4,8]

提示：

1 <= nums.length <= 1000
1 <= nums[i] <= 2 * 10^9
nums 中的所有整数 互不相同

Solution

我们肯定先把这些整数排序吧？这样可以确保后面的数不会干扰前面的数
然后，这里我们着重介绍一下怎么用回溯法求出最长递增子序列
这里写的是，我们根据我们怎么转移出来的，直接根据\(dp\)跟\(nums\)两个数组的关系，倒序加入结果数组中

class Solution {
public:vector<int> largestDivisibleSubset(vector<int>& nums) {int n=nums.size();sort(nums.begin(),nums.end());vector<int>dp(n+5,0);dp[0]=1;for(int i=1;i<=n-1;i++){for(int j=0;j<=i-1;j++){if(nums[i]%nums[j]==0){dp[i]=max(dp[i],dp[j]+1);continue;}dp[i]=max(dp[i],1);}}int maxx=0;int ans=0;for(int i=0;i<=n-1;i++){if(dp[i]>=ans){ans=dp[i];maxx=i;}}vector<int>res;res.push_back(nums[maxx]);ans--;while(ans>0){for(int i=maxx-1;i>=0;i--){if(dp[i]==ans&&nums[maxx]%nums[i]==0){maxx=i;res.push_back(nums[i]);ans--;break;}}}std::reverse(res.begin(),res.end());return res;}
};

2901. 最长相邻不相等子序列 II

给定一个字符串数组 words ，和一个数组 groups ，两个数组长度都是 n 。

两个长度相等字符串的 汉明距离 定义为对应位置字符不同的数目。

你需要从下标 [0, 1, ..., n - 1] 中选出一个 最长子序列 ，将这个子序列记作长度为 k 的 [i0, i1, ..., ik - 1] ，它需要满足以下条件：

相邻下标对应的 groups 值不同。即，对于所有满足 0 < j + 1 < k 的 j 都有 groups[i_j] != groups[i_j + 1] 。
对于所有 0 < j + 1 < k 的下标 j ，都满足 words[i_j] 和 words[i_j + 1] 的长度相等，且两个字符串之间的 汉明距离 为 1 。

请你返回一个字符串数组，它是下标子序列依次对应 words 数组中的字符串连接形成的字符串数组。如果有多个答案，返回任意一个。

子序列 指的是从原数组中删掉一些（也可能一个也不删掉）元素，剩余元素不改变相对位置得到的新的数组。

注意 words 中的字符串长度可能 不相等 。

示例 1：

输入：words = ["bab","dab","cab"], groups = [1,2,2]
输出：["bab","cab"]
解释：一个可行的子序列是 [0,2] 。

groups[0] != groups[2]
words[0].length == words[2].length 且它们之间的汉明距离为 1 。
所以一个可行的答案是 [words[0],words[2]] = ["bab","cab"] 。
另一个可行的子序列是 [0,1] 。
groups[0] != groups[1]
words[0].length = words[1].length 且它们之间的汉明距离为 1 。
所以另一个可行的答案是 [words[0],words[1]] = ["bab","dab"] 。
符合题意的最长子序列的长度为 2 。

示例 2：

输入：words = ["a","b","c","d"], groups = [1,2,3,4]
输出：["a","b","c","d"]
解释：我们选择子序列 [0,1,2,3] 。
它同时满足两个条件。
所以答案为 [words[0],words[1],words[2],words[3]] = ["a","b","c","d"] 。
它是所有下标子序列里最长且满足所有条件的。
所以它是唯一的答案。

提示：

1 <= n == words.length == groups.length <= 1000
1 <= words[i].length <= 10
1 <= groups[i] <= n
words 中的字符串 互不相同 。
words[i] 只包含小写英文字母。

Solution

人话：预处理出汉明距离之间的关系，然后满足选的相邻数不相等
最后回溯出数组就可以了

class Solution {
public:vector<string> getWordsInLongestSubsequence(vector<string>& words, vector<int>& groups) {int n=words.size();vector<vector<bool>>ma(n+5,vector<bool>(n+5,false));for(int i=0;i<=n-1;i++){for(int j=i+1;j<=n-1;j++){if(words[i].length()!=words[j].length()) continue;int flag=0;for(int v=0;v<=words[i].length()-1;v++){if(words[i][v]!=words[j][v]) flag++;}if(flag==0||flag==1){ma[i][j]=true;ma[j][i]=true;}}}vector<int>dp(n+5,0);dp[0]=1;for(int i=1;i<=n-1;i++){for(int j=0;j<=i-1;j++){if(groups[j]!=groups[i]&&ma[i][j]) dp[i]=max(dp[j]+1,dp[i]);else dp[i]=max(dp[i],1);}}int ans=0,maxx=0;for(int i=0;i<=n-1;i++){if(dp[i]>=ans){ans=dp[i];maxx=i;}}vector<string>res;ans--;res.push_back(words[maxx]);while(ans>0){bool found=false;for(int i=maxx-1;i>=0;i--){if(dp[i]==dp[maxx]-1&&groups[i]!=groups[maxx]&&ma[i][maxx]){ans--;res.push_back(words[i]);maxx=i;found=true;break;}}if(!found) break;}std::reverse(res.begin(),res.end());return res;}
};