在计算机科学与运筹优化领域,许多问题因规模庞大或结构复杂而被归类为NP难问题,如旅行商问题、车辆路径规划与生产调度。这类问题用精确算法往往需要指数级时间,难以在实际中求得最优解。启发式算法应运而生,其核心思想是利用问题特征和经验信息,引导搜索过程快速逼近较优解,而非穷举全部解空间。从20世纪50年代西蒙与纽厄尔提出“启发式问题求解”概念起,到A*搜索、遗传算法、蚁群优化等方法的发展,启发式算法逐步演化为智能优化的重要支柱,并在人工智能、机器学习与工业系统中展现出强大生命力。
“在无法穷尽一切可能性的世界中,启发式算法赋予我们一条可行之路。它不追求绝对完美,却能在有限资源中逼近智慧的极限;它让计算机不仅能算,更能‘思考’,在复杂问题的迷雾中找到方向。”
目录
- 一、引言
- 二、历史背景与思想起源
- 三、代表人物与贡献
- 四、核心算法体系
- 五、应用案例与实战
- 六、最新发展与前沿趋势
- 七、方法评价、挑战与未来展望
- 八、结语
- 参考文献
一、引言
在计算机科学与运筹优化领域,许多实际问题存在着惊人的复杂性,例如旅行商问题(TSP)、作业车间调度、物流配送和路径规划等。这些问题通常属于 NP难问题,其解空间随着问题规模指数式增长,呈现出典型的“组合爆炸”特征。面对这种复杂度,传统的 精确算法(如动态规划、分支界限法)虽然能够保证找到全局最优解,但在大规模实例中往往因计算资源和时间的限制而无法实际应用。在此背景下,启发式算法应运而生。它通过引入问题的经验信息与搜索策略,不再盲目遍历全部解,而是利用启发性评估函数引导搜索,快速逼近较优解。虽然结果未必绝对最优,但在工程实践中往往已足够高效且具有可操作性。
本文旨在系统梳理启发式算法的发展脉络与前沿进展:从西蒙提出启发式概念,到遗传算法、蚁群优化等代表方法的兴起,再到现代元启发式与深度学习的融合。读者不仅能了解其 历史背景、代表人物与核心原理,还将洞悉启发式算法在 人工智能与工业优化 中的广泛应用与未来趋势。
二、历史背景与思想起源
2.1 启发式的提出与早期AI探索
“启发式”一词最早由美国人工智能先驱 赫伯特·西蒙(Herbert Simon) 和 艾伦·纽厄尔(Allen Newell) 于20世纪50年代提出。他们试图通过模拟人类问题求解过程,建立计算机能够执行的搜索策略。在这一思想下,他们开发了著名的 通用问题求解器(GPS, General Problem Solver),这是最早的AI系统之一,通过“手段—目的分析”策略分解问题,并以启发式函数引导搜索路径。与传统穷举搜索相比,这种方法显著缩小了搜索空间,为后续算法奠定基础。
在此期间,出现了多种早期AI搜索算法:贪心算法以最小代价优先选择当前最佳路径;爬山算法通过迭代改进逐步逼近目标,但容易陷入局部最优;而1968年提出的 A* 算法结合代价与启发信息,被誉为最具影响力的路径搜索算法,至今仍广泛应用于机器人导航与地图规划。
2.2 认知科学与运筹学的交汇
启发式思想不仅源于计算机科学,也深受 认知心理学 影响。西蒙提出“有限理性”理论,认为人类在有限信息与时间下依赖经验和直觉决策,这一观点启发了计算机启发式策略的设计。同时,运筹学领域的调度、排程问题也开始采用启发式方法解决复杂优化模型,如工厂生产线分配与物流运输,体现了跨学科融合。
2.3 从AI搜索到组合优化的过渡
20世纪80年代后,计算机性能提升与应用需求变化推动启发式算法进入 组合优化 领域。传统AI搜索更关注推理与博弈,而组合优化涉及旅行商问题、车辆路径问题等工业级难题,对算法效率与近似最优解提出更高要求。这一时期涌现出 模拟退火、遗传算法 等元启发式方法,开启了启发式算法从早期AI到现代智能优化的转型。
三、代表人物与贡献
3.1 赫伯特·西蒙(Herbert Simon)
赫伯特·西蒙是启发式算法思想的奠基人之一,他在20世纪50年代与纽厄尔合作提出了“启发式问题求解”的概念,并开发了著名的 通用问题求解器(GPS)。西蒙将人类决策行为建模为有限信息和有限计算能力下的理性选择,提出了著名的 有限理性(Bounded Rationality) 理论。这一理论强调,实际问题求解过程中,人们不会追求绝对最优解,而是依靠经验和启发信息获得“满意解”。这一观点直接影响了启发式算法的发展方向,使其从单纯的数学推理扩展到模拟人类思维模式。西蒙后来因在决策理论和人工智能领域的开创性工作获得诺贝尔经济学奖,其思想至今仍是启发式算法研究的重要基石。
3.2 大卫·哈特与 A* 算法团队
1968年,大卫·哈特(Peter Hart)、尼尔森(Nils Nilsson)和拉斐尔(Bertram Raphael)合作提出了著名的 A* 算法,这是路径搜索领域的里程碑。A* 算法通过结合实际代价和启发估计代价(即 \(f(n) = g(n) + h(n)\))实现最优搜索,大大提升了搜索效率。其优雅的框架不仅适用于图搜索和路径规划,还为后续的多种改进算法(如 IDA*、D* Lite)奠定基础。A* 的出现标志着启发式函数在AI搜索中的成熟应用,并在机器人导航、游戏开发、地图服务中广泛采用。
3.3 约翰·霍兰德(John Holland)与遗传算法
约翰·霍兰德是 遗传算法(Genetic Algorithm, GA) 的创始人,他在20世纪70年代将生物进化中的 选择、交叉、变异 等机制引入计算机优化,开创了进化计算的新方向。霍兰德提出“复杂适应系统”概念,认为自然界适应性进化的规律同样适用于人工系统优化。遗传算法通过群体搜索与概率演化克服了局部最优问题,适用于求解高维非线性复杂问题。霍兰德的研究影响深远,他培养的“密歇根学派”后来在进化算法、人工生命和复杂系统研究领域产生了广泛影响。
3.4 马尔科·多里戈(Marco Dorigo)与蚁群优化
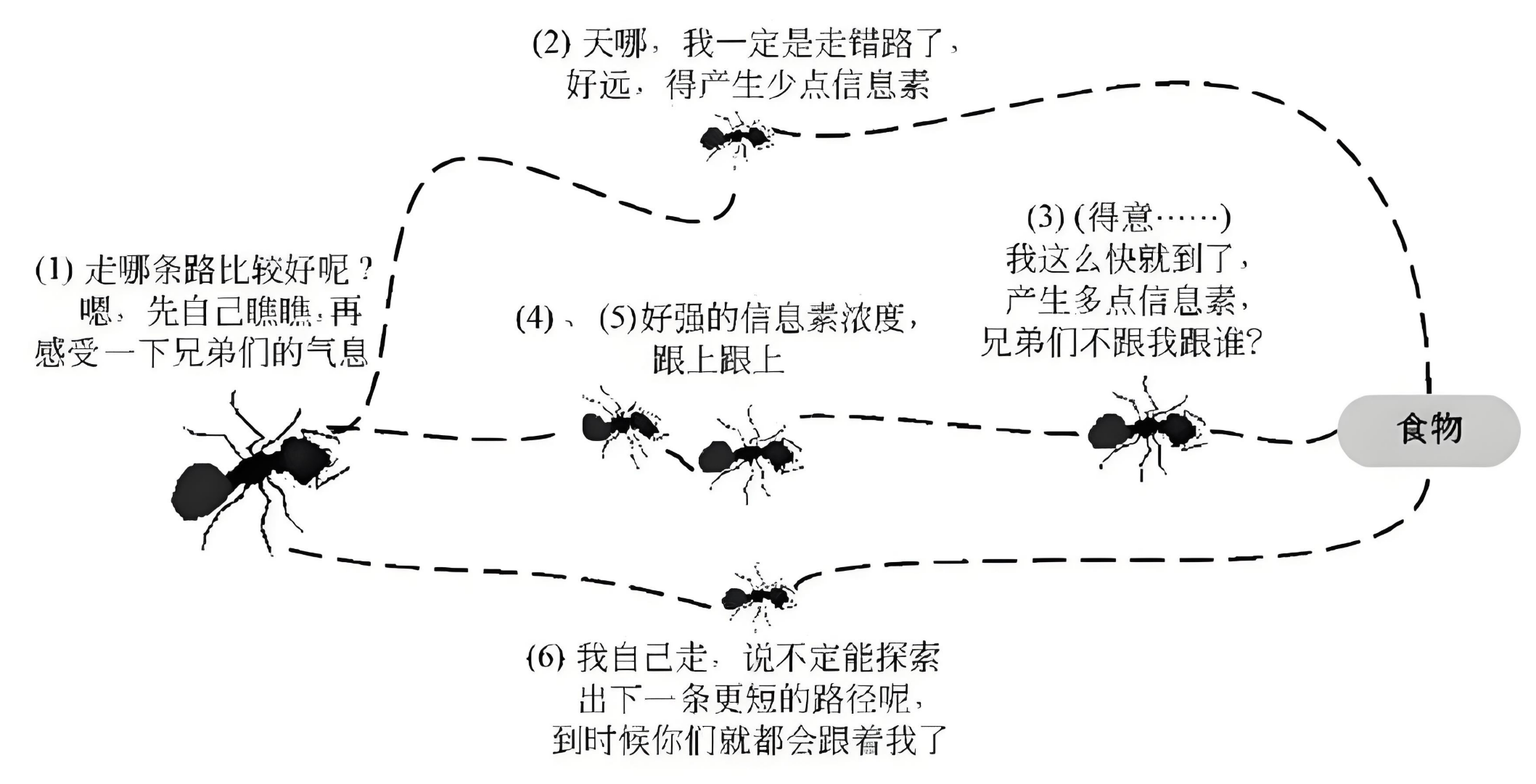
比利时学者马尔科·多里戈于1992年提出 蚁群优化算法(Ant Colony Optimization, ACO),首次将蚂蚁觅食行为中的信息素机制引入计算机算法。该算法模拟蚂蚁在路径上释放和感知信息素,通过正反馈机制逐渐收敛到最优路径。蚁群算法在解决旅行商问题、车辆路径问题、网络路由等组合优化任务中表现出优越性,并开创了群体智能优化的研究浪潮。多里戈及其团队的研究不仅推动了算法本身的演进,还催生了粒子群优化、人工蜂群算法等群体智能方法,使群体行为成为启发式算法的重要研究方向。
四、核心算法体系
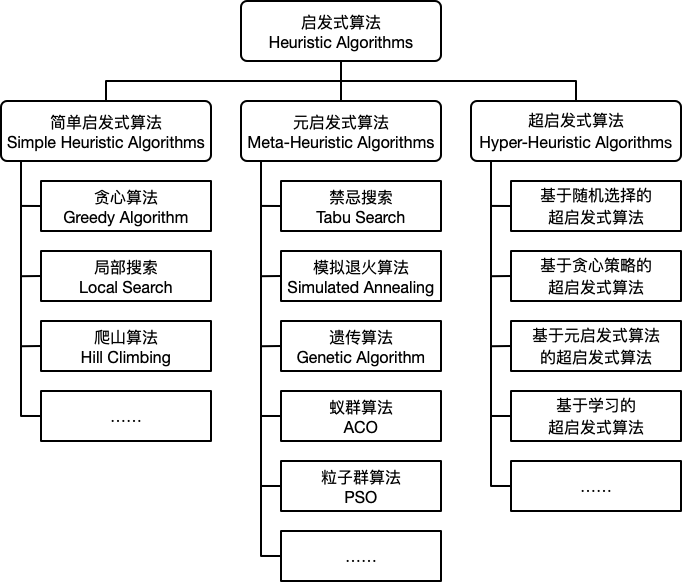
4.1 基础启发式算法
贪心算法是一种简单直观的启发式方法,每一步都选择当前看来最优的解,希望通过局部最优逐步逼近全局最优。其优点是实现简单、计算速度快,常用于图搜索和最短路径问题,如Dijkstra算法即是贪心思想的典型应用。但缺点是容易陷入局部最优,无法回溯或调整,不能保证全局最优解。
爬山算法(Hill Climbing)则通过不断迭代,沿梯度或邻域方向寻找更优解。它改进了贪心的缺陷,能在解空间中向上“爬升”,但仍存在陷入局部极值的风险。为了缓解这一问题,常用随机重启或变种方法增强算法的跳出能力。
最佳优先搜索结合了启发式评估函数,选择代价估计最低的节点优先扩展。A*算法即是其中典型代表,广泛应用于路径规划。**迭代加深搜索(Iterative Deepening Search)**则结合深度优先搜索的空间优势与广度优先的完整性,逐层加深搜索深度,有效平衡时间与空间资源。
4.2 元启发式算法
元启发式算法指设计灵活、通用性强的高层优化策略,能应用于不同问题,通常结合随机性和局部搜索以避免陷入局部最优。
**模拟退火(Simulated Annealing, SA)**模仿物理退火过程,通过控制“温度”逐渐降低接受劣解的概率,平衡探索与利用,广泛应用于旅行商等组合优化问题。
**遗传算法(Genetic Algorithm, GA)**基于自然选择与遗传学原理,通过编码、选择、交叉和变异操作对解空间进行群体式搜索,特别适合处理复杂、多峰问题。
**蚁群优化(Ant Colony Optimization, ACO)**模拟蚂蚁释放信息素路径选择行为,利用正反馈机制逐步优化路径,尤其适合解决路径规划和网络路由问题。
**粒子群优化(Particle Swarm Optimization, PSO)**受到鸟群觅食行为启发,每个“粒子”根据自身经验和群体经验调整速度与位置,快速收敛于多维连续空间的最优解。
4.3 算法对比表格
| 算法类别 | 优点 | 缺点 | 适用场景 |
|---|---|---|---|
| 贪心算法 | 简单、快速 | 易陷入局部最优 | 最短路径、资源分配 |
| 爬山算法 | 迭代改进,收敛速度快 | 容易陷入局部极值 | 参数调优、小规模问题 |
| A*搜索 | 保证最优解、启发式指导强 | 依赖启发函数,空间复杂度高 | 路径规划、游戏AI |
| 模拟退火 | 跳出局部极值,通用性好 | 参数调节复杂,收敛速度慢 | 旅行商、调度问题 |
| 遗传算法 | 群体搜索、适合复杂问题 | 收敛慢,参数调整困难 | 多峰优化、机器学习超参调整 |
| 蚁群优化 | 自适应信息素,适合路径问题 | 计算开销大,易陷入早熟收敛 | 网络路由、物流调度 |
| 粒子群优化 | 收敛速度快,易实现 | 容易早熟收敛,局部极值问题 | 连续优化、多维函数搜索 |
| 精确算法 | 可保证全局最优 | 计算资源消耗极大 | 小规模问题、精度要求高场合 |
这张对比表展示了不同算法在性能、适用性上的权衡,为实际问题选择合适启发式或元启发式算法提供参考。
五、应用案例与实战
5.1 路径规划
路径规划是启发式算法最经典的应用场景之一,尤其在机器人导航和智能交通系统中具有重要价值。
机器人路径搜索:A* 与蚁群优化对比
A*算法结合了实际路径代价 \(g(n)\) 和启发式估价函数 \(h(n)\),其评价函数为:
其中,\(g(n)\) 表示从起点到当前节点 \(n\) 的实际代价,\(h(n)\) 是节点 \(n\) 到目标节点的启发式估计距离。A*通过优先扩展具有最低 \(f(n)\) 值的节点,有效避免了盲目搜索。该算法保证在启发函数 \(h(n)\) 满足一致性条件时找到最优路径,且搜索效率较高。
蚁群优化(ACO)则模拟蚂蚁释放信息素的行为,路径选择概率由信息素强度 \(\tau_{ij}\) 和启发函数 \(\eta_{ij}\) 共同决定:
其中,\(\alpha\) 和 \(\beta\) 分别控制信息素和启发函数的重要性,\(N_i\) 是节点 \(i\) 的邻居集。ACO 通过迭代更新信息素,逐步强化高质量路径。相比A*,ACO更适合解决动态环境下的路径规划和多目标优化问题,但计算成本较高。
城市交通导航与动态障碍问题
在城市交通导航中,路径规划需要应对路况实时变化、交通拥堵和突发障碍。基于A*的动态路径调整算法(如D* Lite)能够快速响应环境变化,而ACO等群体智能算法则通过多智能体协同优化路径,提升导航系统的鲁棒性和灵活性。
5.2 调度优化
调度问题广泛存在于制造业、物流和服务业,启发式算法成为求解复杂调度任务的有效工具。
生产排程问题(车间调度)
车间调度问题(Job Shop Scheduling Problem, JSSP)旨在合理安排多工序、多机器的作业顺序,以最小化总完工时间或延迟。由于JSSP属于NP难问题,精确算法难以处理大规模实例。
启发式方法如遗传算法通过编码作业顺序,设计合适的交叉和变异操作,生成高质量调度方案。遗传算法的适应度函数通常定义为:
其中,\(C_{max}\) 为调度完成的最大完工时间。通过选择适应度高的个体进行迭代,遗传算法逐渐逼近优化调度方案。
车辆路径问题(Vehicle Routing Problem, VRP)
VRP关注如何设计车辆路线以满足客户需求,降低运输成本。蚁群算法和粒子群优化在VRP中表现优异。蚁群算法通过模拟蚂蚁寻找路径的行为,适应动态路况;粒子群优化则通过群体协同调整路径,实现快速收敛。
5.3 机器学习与超参数优化
启发式算法在机器学习中的应用越来越广泛,尤其在模型超参数调优领域。
遗传算法与神经网络参数搜索
神经网络训练过程中,超参数如学习率、隐藏层数和节点数等对模型性能影响巨大。遗传算法通过编码超参数为基因串,利用选择、交叉、变异机制搜索最优配置。适应度函数一般定义为验证集上的准确率或误差倒数:
此方法避免了手工调参的盲目性,提高了模型的泛化能力。
粒子群优化在深度学习中的应用
粒子群优化(PSO)以群体搜索方式优化神经网络权重和超参数。每个粒子表示一个候选解,其位置和速度更新公式为:
其中,\(v_i\) 和 \(x_i\) 分别为粒子速度和位置,\(pbest_i\) 为个体历史最佳位置,\(gbest\) 为全局最佳位置,\(w\) 是惯性权重,\(c_1, c_2\) 是学习因子,\(r_1, r_2\) 为随机数。PSO简化了参数空间搜索流程,提升训练效率。
以上案例展示了启发式算法在多个复杂场景中的灵活应用,结合数学模型与算法机制,促进了智能系统的实用性与效率提升。
六、最新发展与前沿趋势
6.1 与深度学习结合
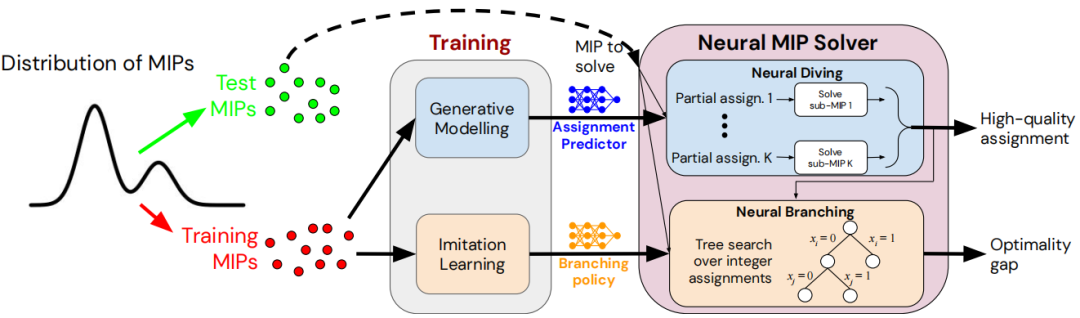
近年来,启发式算法与深度学习的融合成为研究热点。深度强化学习(Deep Reinforcement Learning, DRL)结合了强化学习与深度神经网络,利用启发式策略优化决策过程。DRL通过与环境的交互不断调整策略,使智能体在复杂动态环境中自适应地探索最优路径和动作序列。这种结合不仅提升了传统强化学习在高维状态空间中的表现,也为启发式算法注入了强大的数据驱动力和泛化能力。
另一重要方向是神经架构搜索(Neural Architecture Search, NAS),即利用启发式和元学习技术自动设计神经网络结构。NAS通过搜索算法(如遗传算法、强化学习、贝叶斯优化)在庞大的模型空间中高效寻找性能最优的架构,极大地减少了人工设计神经网络的工作量。此外,元学习(Meta-learning)作为“学习如何学习”的方法,融合启发式优化策略,使算法能快速适应新任务,进一步推动智能算法的自动化与泛化。
6.2 混合与自适应启发式
为提升算法性能,研究者提出多种混合启发式方法,结合不同启发式算法的优势。例如,遗传算法与局部搜索相结合,利用遗传算法进行全局探索,局部搜索强化局部精细调优。这类混合策略在许多复杂优化问题中展现出更强的搜索能力和鲁棒性。
同时,参数自适应与在线调整成为提升启发式算法智能化的重要手段。传统算法参数通常固定,而自适应机制通过实时反馈自动调整算法参数(如变异率、信息素挥发率、搜索步长),实现动态平衡探索与开发,提高收敛速度与解的质量。这种自适应方法广泛应用于粒子群优化、蚁群优化等元启发式算法。
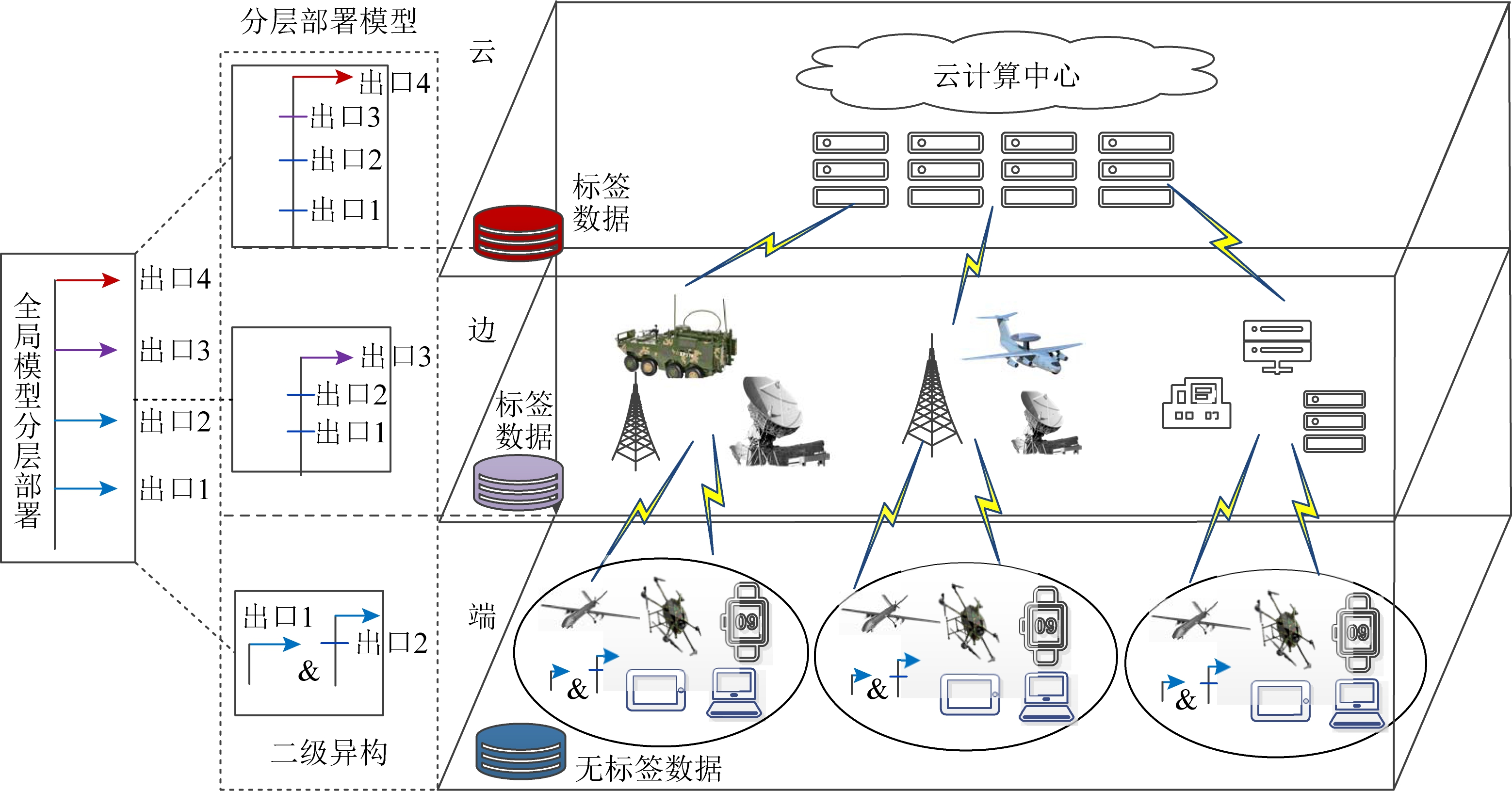
6.3 面向大规模计算与分布式优化
随着问题规模和数据量急剧增长,启发式算法面临计算资源的巨大挑战。GPU加速与并行计算成为关键技术,通过利用GPU强大的并行处理能力,显著缩短了算法运行时间。例如,基于CUDA的粒子群和遗传算法实现,使数百万粒子的群体搜索成为可能。
此外,云计算环境为启发式算法提供了弹性算力支持。分布式启发式算法利用集群资源并行搜索,提高了算法的扩展性和容错性。研究者开发了多种分布式框架,实现多节点协同进化和信息共享,广泛应用于大规模工业优化和智能调度。
6.4 量子启发式算法
量子计算的兴起为启发式算法注入了新活力。量子退火(Quantum Annealing)利用量子叠加和隧穿效应,帮助算法跳出局部最优,寻找全局最优解。量子退火机如D-Wave已在组合优化和机器学习中展示潜力。未来,结合量子算法和经典启发式方法的混合模型,可能推动解决传统计算难以处理的超大规模问题。
七、方法评价、挑战与未来展望
7.1 方法评价
启发式算法的性能评估主要集中在以下几个方面:
- 收敛速度:衡量算法在有限时间内找到较优解的效率,是实际应用中非常关键的指标。
- 稳定性:反映算法在多次运行中结果的重复性和鲁棒性,确保优化结果的可靠性。
- 泛化能力:考察算法在不同问题实例和环境中适应并保持良好性能的能力。
这三者之间往往需要权衡,例如提升收敛速度可能会牺牲一定的稳定性,而增强泛化能力有时会导致对特定问题的优化效果下降。
相比于传统的精确算法(如动态规划、分支界限法),启发式算法虽然不能保证找到全局最优解,但在大规模和复杂问题上展现出更好的实用性和扩展性。其灵活的设计和多样化策略使其易于适配多种应用场景,并且能与其他智能算法相结合,提高整体性能。
7.2 挑战
启发式算法当前面临多方面挑战:
- 经验依赖性强:算法设计和启发函数构造高度依赖专家经验,限制了算法的通用性。
- 参数调节复杂:算法参数众多且相互影响,缺乏统一的理论指导,调参过程耗时耗力。
- 自动化程度不足:缺乏高效的自适应机制和自动调节能力,难以在不同场景下快速调整。
解决上述问题,推动启发式算法向自动化、自适应方向发展,是当前研究的重点。
7.3 未来展望
随着AI 2.0时代的来临,启发式算法迎来了新的发展契机。结合大数据、云计算和深度学习,启发式算法将实现更高层次的智能化和自动化,尤其在自动驾驶、智能制造、智慧城市等复杂系统中发挥核心作用。
未来的研究趋势还包括:
- 算法可解释性与透明性:满足社会对公平、公正和可理解算法的需求,推动启发式算法向可解释人工智能方向发展。
- 跨学科融合:将数学、认知科学、生物学等领域的理论与技术融入启发式算法,拓宽应用边界。
- 新兴技术结合:如量子计算、分布式计算等技术的结合,提升算法在超大规模优化中的能力。
综上所述,启发式算法将在理论创新与实际应用中持续突破,成为智能优化领域的重要支柱。
结语
启发式算法作为智能优化领域的重要思想,自诞生以来不断演进,从最初的简单启发搜索到如今融合元启发式方法与深度学习技术,极大地拓展了复杂问题的解决边界。它突破了传统精确算法在大规模、复杂环境中的计算瓶颈,以灵活、高效和适应性强的特点,成为工程技术和科学研究中不可或缺的工具。更深层次地,启发式算法体现了“有限理性”理论与“经验智慧”的有机结合,模拟了人类决策过程中的直觉与经验,赋予智能系统更强的现实适应能力。随着人工智能和计算资源的不断发展,启发式算法将在理论创新、自适应设计和跨学科应用等方面持续深化,为自动驾驶、智能制造、医疗诊断等关键领域提供坚实支撑,推动智能优化迈向更高水平。
参考文献
- Simon, H. A. (1957). Models of Man: Social and Rational. Wiley.
- Hart, P. E., Nilsson, N. J., & Raphael, B. (1968). "A Formal Basis for the Heuristic Determination of Minimum Cost Paths." IEEE Transactions on Systems Science and Cybernetics, 4(2), 100–107.
- Holland, J. H. (1975). Adaptation in Natural and Artificial Systems. University of Michigan Press.
- Dorigo, M., & Stützle, T. (2004). Ant Colony Optimization. MIT Press.
- Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press.
启发式算法融合了经验与智能,突破了传统优化的局限。它以灵活高效的策略,解决复杂难题,成为智能系统的核心引擎。
