manacher 马拉车算法 寻找最长回文子串
例题
洛谷 P3805 【模板】manacher

回文串的定义
回文串是字符串中常见的一种,一个字符串是回文串代表这个字符串
从前往后和从后往前读是相等的,形式化定义就是一个长为 \(n\) 字符串
\(S\) 是回文的当且仅当对于任意 i,有 \(S_i = S_n−i+1\)
回文串的性质:一个回文串左右同时加一个字符,得到
的仍然是回文串。
启示
可以从一个中心开始向左右拓展,添加字符,能拓展就拓展,拓展不了那么说明以这个为中心的
更长的串一定也不是回文串。于是对于每一个中心点 \(c\),我们都存在一个最长回文半径 \(r\)。
如图
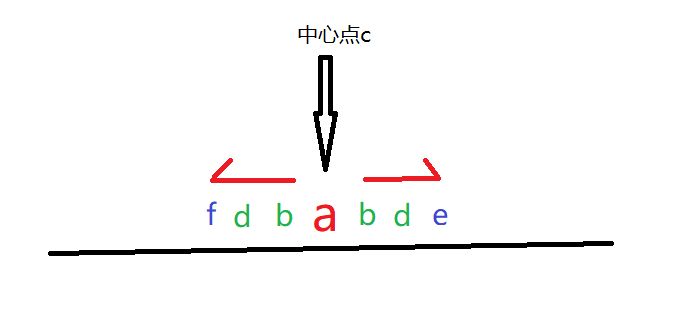
中心点为a, 最长回文半径是3,绿色为可扩展字符,蓝色为不可扩展字符
奇偶串的处理
有些串的中心在两个字符中间,而有些串的中心正好是一个字符。为了方便起见,我们可以先在每个字符中间加入一个分割符,这样原串中所有的回文串就都以一个字符为中心了。
大概就是,假如我们现在有一个字符串 \(S = racecar\),我们就可以将
它变成一个字符串 \(S = |r|a|c|e|c|a|r|\)。
答案统计
接下来只考虑以某个位置为中心的最长回文串半径 \(r_i\)(即最长回文串为 \(S[i − r_i + 1, i + r_i − 1]\)),原串的最长回文串长度就等于\(r_i − 1\)(因为中间加了分隔符),以该字符为中心的回文串有\(\llcorner r_i/2\lrcorner\) 。
算法原理
如果一个长回文串中有一个子回文串,那么这个子回文串翻转过后的位置一定也是一个回文串。
如图
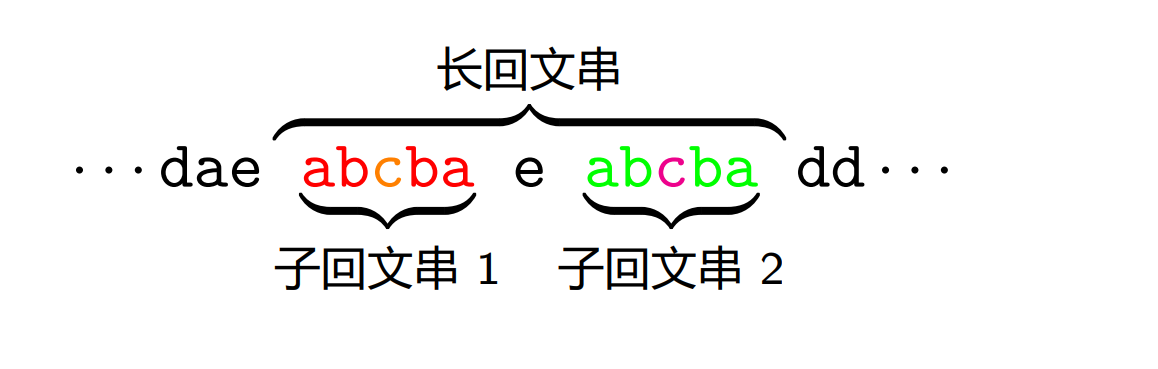
记录当前最长的一个回文串(右端点最靠右),这样当我们寻找以当前字符 \(c\) 为中心的最长回文串时,我们可以直接用 \(c'\) 为中心的最长子回文串的半径为初始值( \(c'\) 为当前字符 \(c\) 在最长回文串的对称点),然后在这基础上再进行拓展。需要注意的是,以 \(c\) 为中心的最长回文串实际上是 \(aeabcbaea\),是比长回文串更长的,所以我们需要把它缩减到长回文串内部再进行拓展,所以需要取一个 min。
如果当前中心已经不在最长回文串内了,那就直接从当前点 \(c\) (r为1) 开始拓展。
时间复杂度:\(O(n)\)
代码
#include<bits/stdc++.h>
using namespace std;
char t[22000010];//加了分隔符的串
int l[22000010];//以i为中心点的回文串的半径
int main()
{string s;cin>>s;t[1]='|';//分隔符,避免区分奇偶串 int n=s.size();for(int i=1;i<=n;i++){t[2*i]=s[i-1];t[2*i+1]='|';}n=2*n+1;int c=0,r=-1;//c:最靠右的回文串的中心点,r:遍历过的串的最右右端点 int ans=0;//答案即最长回文串的长度 for(int i=1;i<=n;i++)//枚举中心点 {if(i<=r)//中心点在之前最右回文串的右端点之前,即可以通过之前的状态进行转移 {l[i]=min(l[2*c-i],r-i);//以i为中心点的半径是i关于c的对称点为中心点的回文串的半径和i与r距离的较小值 }else{l[i]=1;//扩展初始值为1 }while(i-l[i]>=1&&i+l[i]<=n&&t[i+l[i]]==t[i-l[i]])//子串被包含且构成回文,利用的是回文串的性质 {l[i]++;//半径加一 }if(i+l[i]-1>r)//中心点加半径大于遍历过的串的最右右端点{c=i;//更新中心点 r=i+l[i]-1;//更新最右右端点 } ans=max(ans,l[i]-1);//更新答案 }cout<<ans;return 0;
}
